

Der Rot-Schwarz-Baum ist eine weit verbreitete konkrete Implementierung eines selbstbalancierenden binären Suchbaums. Im JDK wird er in der TreeMap und seit Java 8 auch bei Bucket-Kollisionen in der HashMap verwendet. Wie funktioniert er?
In diesem Artikel erfährst du:
- Was ist ein Rot-Schwarz-Baum?
- Wie fügt man Elemente in einen Rot-Schwarz-Baum ein? Wie entfernt man sie?
- Nach welchen Regeln wird ein Rot-Schwarz-Baum balanciert?
- Wie implementiert man einen Rot-Schwarz-Baum in Java?
- Wie bestimmt man die Zeitkomplexität?
- Was unterscheidet einen Rot-Schwarz-Baum von anderen Datenstrukturen?
Den Quellcode zum Artikel findest du in diesem GitHub-Repository.
Was ist ein Rot-Schwarz-Baum?
Ein Rot-Schwarz-Baum ist ein selbstbalancierender binärer Suchbaum, d. h. ein binärer Suchbaum, der automatisch eine gewisse Balance aufrechterhält.
Jedem Knoten ist eine Farbe (rot oder schwarz) zugewiesen. Ein Satz von Regeln legt fest, wie diese Farben angeordnet sein müssen (z. B. darf ein roter Knoten keine roten Kinder haben). Durch diese Anordnung wird sichergestellt, dass der Baum eine gewisse Balance erhält.
Nach dem Einfügen und Löschen von Knoten werden recht komplexe Algorithmen angewendet, um die Einhaltung der Regeln zu überprüfen – und bei Abweichungen die vorgeschriebenen Eigenschaften durch Umfärben von Knoten und Rotationen wiederherzustellen.
NIL-Knoten im Rot-Schwarz-Baum
Rot-Schwarz-Bäume werden in der Literatur mit und ohne sogenannte NIL-Knoten dargestellt. Ein NIL-Knoten ist ein Blatt, das keinen Wert enthält. NIL-Knoten werden im späteren Verlauf für die Algorithmen relevant, um z. B. Farben von Onkel- oder Geschwister-Knoten zu bestimmen.
In Java können NIL-Knoten einfach durch null-Referenzen dargestellt werden; dazu später mehr.
Beispiel für einen Rot-Schwarz-Baum
Im folgenden Beispiel siehst du zwei mögliche Darstellungen eines Rot-Schwarz-Baums. Die erste Grafik zeigt den Baum ohne (d. h. mit impliziten) NIL- Blättern; die zweite Grafik zeigt den Baum mit expliziten NIL-Blättern.

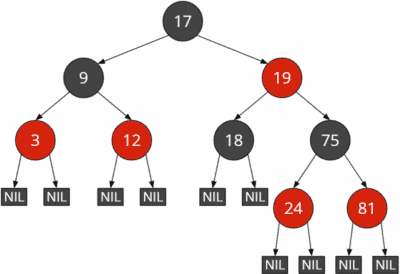
Im Verlauf dieses Artikels werde ich auf die Darstellung der NIL-Blätter in der Regel verzichten. Bei der Erklärung der Einfüge- und Löschoperationen werde ich sie vereinzelt anzeigen, wenn es das Verständnis des jeweiligen Algorithmus erleichert.
Eigenschaften eines Rot-Schwarz-Baums
Die Balance des Rot-Schwarz-Baums wird durch folgende Regeln sichergestellt:
- Jeder Knoten ist entweder rot oder schwarz.
- (Die Wurzel ist schwarz.)
- Alle NIL-Blätter sind schwarz.
- Ein roter Knoten darf keine roten Kinder haben.
- Alle Pfade von einem Knoten zu den darunterliegenden Blättern enthalten die gleiche Anzahl schwarzer Knoten.
Regel 2 steht in Klammern, da sie auf die Balance des Baumes keinerlei Auswirkung hat. Wenn ein Kind einer roten Wurzel ebenfalls rot ist, muss die Wurzel laut Regel 4 schwarz gefärbt werden. Wenn eine rote Wurzel allerdings nur schwarze Kinder hat, bringt es keinen Vorteil die Wurzel schwarz zu färben.
Von daher wird Regel 2 in der Literatur oft weggelassen.
Ich werde in der Erklärung der Einfüge- und Löschoperationen und im Java-Code darauf hinweisen, wo es Unterschiede gäbe, wenn auch Regel 2 umgesetzt würde. Soviel im Voraus: Der Unterschied ist pro Operation nur eine Zeile Code :)
Aus Regeln 4 und 5 folgt übrigens, dass ein roter Knoten immer entweder zwei NIL-Blätter hat oder zwei schwarze Kind-Knoten mit Werten. Hätte er ein NIL-Blatt und ein schwarzes Kind mit Wert, dann würden die Pfade durch dieses Kind mindestens einen schwarzen Knoten mehr haben als der Pfad zum NIL-Blatt, und das würde Regel 5 verletzen.
Höhe des Rot-Schwarz-Baums
Als Höhe des Rot-Schwarz-Baums bezeichnen wir die maximale Anzahl an Knoten von der Wurzel bis zu einem NIL-Blatt, die Wurzel nicht eingerechnet. Die Höhe des Rot-Schwarz-Baums im Beispiel oben beträgt 4:

Aus Regeln 3 und 4 folgt:
Der längste Pfad von der Wurzel zu einem Blatt (die Wurzel nicht eingerechnet) ist maximal doppelt so lang wie der kürzeste Pfad von der Wurzel zu einem Blatt.
Dies ist einfach erklärt:
Nehmen wir an, der kürzeste Pfad hat (zusätzlich zur Wurzel) n schwarze und keine roten Knoten. Dann könnten wir noch einmal n rote Knoten vor jedem schwarzen Knoten einfügen, ohne Regel 3 zu brechen (die man auch umformulieren könnte in: es dürfen keine zwei rote Knoten aufeinander folgen).
Das folgende Beispiel zeigt links den kürzestestmöglichen Pfad und rechts den längstmöglichen Pfad durch einen Rot-Schwarz-Baum der Höhe 4:

Die Pfade zu den NIL-Blättern links haben eine Länge (exklusive Wurzel) von 2; die Pfade zu den NIL-Blättern rechts unten haben eine Länge von 4.
Schwarz-Höhe des Rot-Schwarz-Baums
Als Schwarz-Höhe bezeichnet man die Anzahl schwarzer Knoten von einem bestimmten Knoten bis zu seinen Blättern. Die schwarzen NIL-Blätter werden dabei mitgezählt, der Startknoten nicht.
Die Schwarz-Höhe des gesamten Baumes ist die Anzahl der schwarzen Knoten von der Wurzel (diese wird nicht mitgezählt) bis zu den NIL-Blättern.
Die Schwarz-Höhe aller bisher gezeigten Rot-Schwarz-Bäume ist 2.
Implementierung eines Rot-Schwarz-Baums in Java
Als Ausgangspunkt für für die Implementierung des Rot-Schwarz-Baums in Java verwende ich den Java-Quellcode für den binären Suchbaum aus dem zweiten Teil der Binärbaum-Serie.
Knoten werden durch die Klasse Node dargestellt. Als Knotenwert verwenden wir der Einfachheit halber int-Primitive.
Neben den Kind-Knoten left und right benötigen wir für die Implementierung des Rot-Schwarz-Baums eine Referenz auf den Elternknoten parent sowie die Farbe des Knotens, color. Diese speichern wir in einem boolean, wobei wir rot als false festlegen und schwarz als true.
public class Node {
int data;
Node left;
Node right;
Node parent;
boolean color;
public Node(int data) {
this.data = data;
}
}Code-Sprache: Java (java)Den Rot-Schwarz-Baum implementieren wir in der Klasse RedBlackTree. Diese erweitert die im zweiten Teil der Serie vorgestellte Klasse BaseBinaryTree (die im Wesentlichen eine getRoot()-Funktion zur Verfügung stellt).
Die Operationen (Einfügen, Suche, Löschen) werden in den folgenden Abschnitten nach und nach hinzugefügt.
Doch zunächst müssen wir einige Hilfsfunktionen definieren.
Rot-Schwarz-Baum Rotation
Einfügen und Löschen funktioniert grundsätzlich so wie im Artikel über binäre Suchbäume beschrieben.
Nach dem Einfügen und Löschen werden die Rot-Schwarz-Regeln (s. o.) überprüft. Wenn diese verletzt wurden, müssen sie wiederhergestellt werden. Dies geschieht durch Umfärben von Knoten und durch Rotationen.
Die Rotation funktioniert exakt wie bei den AVL-Bäumen, die ich im vorangegangenen Tutorial beschrieben habe. Ich zeige dir hier noch einmal die entsprechenden Diagramme. Ausführliche Erklärungen findest du im Abschnitt "AVL-Baum-Rotationen" des eben genannten Artikels.
Rechts-Rotation
Die folgende Grafik zeigt eine Rechts-Rotation. Die Farben haben keinen Bezug zu denen des Rot-Schwarz-Baumes. Sie dienen lediglich der besseren Nachverfolgung der Knotenbewegungen.
Der linke Knoten L wird zur neuen Wurzel, die Wurzel N zu dessen rechtem Kind. Das rechte Kind LR des vor der Rotation linken Knotens L wird zum linken Kind des nach der Rotation rechten Knotens N. Die zwei weißen Knoten LL und R ändern ihre relative Position nicht.

Der Java-Code ist etwas länger als beim AVL-Baum – aus folgenden zwei Gründen:
- Wir müssen auch die
parent-Referenzen der Knoten aktualisieren (im AVL-Baum haben wir ohneparent-Referenzen gearbeitet). - Wir müssen die Referenzen von und zum Eltern-Knoten desjenigen Knotens, der zu Beginn der Rotation oben liegt (in der Grafik N), aktualisieren. Dies geschah beim AVL-Baum indirekt durch das Zurückgeben der neuen Wurzel des rotierten Teilbaums und das "Einhängen" der Rotation in den rekursiven Aufruf der Einfüge- und Lösch-Operationen.
Die Implementierung der Rechts-Rotation findest du im Quellcode ab Zeile 358:
private void rotateRight(Node node) {
Node parent = node.parent;
Node leftChild = node.left;
node.left = leftChild.right;
if (leftChild.right != null) {
leftChild.right.parent = node;
}
leftChild.right = node;
node.parent = leftChild;
replaceParentsChild(parent, node, leftChild);
}Code-Sprache: Java (java)Die am Ende aufgerufene Methode replaceParentsChild() setzt die Eltern-Kind-Beziehung zwischen dem Eltern-Knoten des ehemaligen Wurzelknotens N des rotierten Teilbaums und dessen neuen Wurzelknoten L. Du findest sie im Code ab Zeile 388:
private void replaceParentsChild(Node parent, Node oldChild, Node newChild) {
if (parent == null) {
root = newChild;
} else if (parent.left == oldChild) {
parent.left = newChild;
} else if (parent.right == oldChild) {
parent.right = newChild;
} else {
throw new IllegalStateException("Node is not a child of its parent");
}
if (newChild != null) {
newChild.parent = parent;
}
}Code-Sprache: Java (java)Links-Rotation
Die Links-Rotation funktioniert analog: Der rechte Knoten R wandert hoch an die Spitze. Die Wurzel N wird zum linken Kind von R. Das linke Kind RL des ehemals rechten Knotens R wird zum rechten Kind des nach der Rotation linken Knotens N. L und RR ändern ihre relative Position nicht.

Hier ist der Java-Code für die Links-Rotation (Quellcode ab Zeile 373):
private void rotateLeft(Node node) {
Node parent = node.parent;
Node rightChild = node.right;
node.right = rightChild.left;
if (rightChild.left != null) {
rightChild.left.parent = node;
}
rightChild.left = node;
node.parent = rightChild;
replaceParentsChild(parent, node, rightChild);
}Code-Sprache: Java (java)Operationen im Rot-Schwarz-Baum
Wie jeder Binärbaum bietet auch der Rot-Schwarz-Baum Operationen zum Suchen, Einfügen und Löschen von Knoten. Diese gehen wir in den folgenden Abschnitten Schritt für Schritt durch.
An dieser Stelle möchte ich dir den Rot-Schwarz-Baum-Simulator von David Galles empfehlen. Mit diesem kannst du beliebige Einfüge-, Lösch- und Suchoperationen grafisch animiert darstellen.
Suche im Rot-Schwarz-Baum
Die Suche funktioniert wie in jedem binären Suchbaum: Wir vergleichen den Suchschlüssel zunächst mit der Wurzel. Ist der Suchschlüssel kleiner, setzen wir die Suche im linken Teilbaum fort; ist der Suchschlüssel größer, setzen wir die Suche im rechten Teilbaum fort.
Dies wiederholen wir solange, bis wir entweder den gesuchten Knoten gefunden haben – oder bis wir ein NIL-Blatt (im Java-Code: eine null-Referenz) erreicht haben. Das bedeutet dann, dass der gesuchte Schlüssel im Baum nicht existiert.
Eine grafische Darstellung der Suche findest du im Beispiel des Artikels über binäre Suchbäume.
Für den Rot-Schwarz-Baum implementieren wir eine iterative Variante der Suche. Du findest sie im Quellcode ab Zeile 14:
public Node searchNode(int key) {
Node node = root;
while (node != null) {
if (key == node.data) {
return node;
} else if (key < node.data) {
node = node.left;
} else {
node = node.right;
}
}
return null;
}Code-Sprache: Java (java)Der Code sollte selbsterklärend sein.
Im Abschnitt "Suche im binären Suchbaum" des o. g. Artikels findest du auch eine rekursive Version der Suche.
Einfügen in einen Rot-Schwarz-Baum
Um einen neuen Knoten einzufügen, gehen wir zunächst so vor wie im Abschnitt "Einfügen im binären Suchbaum" des entsprechenden Artikels beschrieben. D. h. wir suchen von der Wurzel abwärts die Einfügeposition und hängen den neuen Knoten an ein Blatt oder Halbblatt an.
Den Code findest du in der Klasse RedBlackTree ab Zeile 29:
public void insertNode(int key) {
Node node = root;
Node parent = null;
// Traverse the tree to the left or right depending on the key
while (node != null) {
parent = node;
if (key < node.data) {
node = node.left;
} else if (key > node.data) {
node = node.right;
} else {
throw new IllegalArgumentException("BST already contains a node with key " + key);
}
}
// Insert new node
Node newNode = new Node(key);
newNode.color = RED;
if (parent == null) {
root = newNode;
} else if (key < parent.data) {
parent.left = newNode;
} else {
parent.right = newNode;
}
newNode.parent = parent;
fixRedBlackPropertiesAfterInsert(newNode);
}
Code-Sprache: Java (java)Den neuen Knoten färben wir initial rot, so dass Regel 5 erfüllt ist, d. h. dass alle Pfade auch nach dem Einfügen die gleiche Anzahl schwarzer Knoten aufweisen.
Wenn der Elternknoten des eingefügten Knotens allerdings ebenfalls rot ist, haben wir Regel 4 verletzt. Wir müssen dann durch Umfärben und/oder Rotationen den Baum so reparieren, dass alle Regeln wieder erfüllt sind. Dies geschieht in der Methode fixRedBlackPropertiesAfterInsert(), die in der letzten Zeile der insertNode()-Methode aufgerufen wird.
Bei der Reparatur müssen wir fünf unterschiedliche Fälle behandeln:
- Fall 1: Neuer Knoten ist die Wurzel
- Fall 2: Elternknoten ist rot und die Wurzel
- Fall 3: Elternknoten und Onkelknoten sind rot
- Fall 4: Elternknoten ist rot, Onkelknoten ist schwarz, eingefügter Knoten ist "innerer Enkel"
- Fall 5: Elternknoten ist rot, Onkelknoten ist schwarz, eingefügter Knoten ist "äußerer Enkel"
Die fünf Fälle werden im folgenden beschrieben.
Fall 1: Neuer Knoten ist die Wurzel
Sollte der neue Knoten die Wurzel sein, müssen wir nichts weiter tun. Es sein denn, wir arbeiten mit Regel 2 ("die Wurzel ist immer schwarz"). Dann müssten wir die Wurzel schwarz färben.
Fall 2: Elternknoten ist rot und die Wurzel
In diesem Fall ist Regel 4 verletzt ("kein rot-rot!"). Wir müssen nun lediglich die Wurzel schwarz färben. Dies führt dazu, dass Regel 4 wieder eingehalten wird.

Und Regel 5? Da die Wurzel bei dieser Regel nicht mitgezählt wird, haben alle Pfade nach wie vor einen schwarzen Knoten (die in der Grafik nicht eingezeichneten NIL-Blätter). Und würden wir die Wurzel mitzählen, dann hätten alle Pfade jetzt zwei statt einen schwarze Knoten – auch das wäre erlaubt.
Wenn wir mit Regel 2 arbeiten ("die Wurzel ist immer schwarz"), dann haben wir die Wurzel bereits in Fall 1 schwarz gefärbt, und Fall 2 kann nicht mehr eintreten.
Fall 3: Elternknoten und Onkelknoten sind rot
Als Onkelknoten bezeichnen wir den Geschwisterknoten des Elternknotens, also das zweite Kind des Großelternknotens neben dem Elternknoten. Die folgende Grafik sollte das verständlich machen: Eingefügt wurde die 81; deren Elternknoten ist die 75, der Großelternknoten die 19 und der Onkel die 18.
Sowohl der Elternknoten als auch der Onkelknoten sind rot. In diesem Fall machen wir folgendes:
Wir färben Eltern- und Onkelknoten (im Beispiel 18 und 75) schwarz und den Großelternknoten (im Beispiel 19) rot. Damit ist Regel 4 ("kein rot-rot!") am eingefügten Knoten wieder erfüllt. Die Anzahl schwarzer Knoten pro Pfad ändert sich nicht (im Beispiel bleibt sie bei 2).

Allerdings könnte es nun am Großelternknoten zu zwei roten Knoten in Folge kommen – nämlich dann, wenn auch der Urgroßelternknoten (im Beispiel die 17) rot wäre. In diesem Fall müssten wir weitere Reparaturen vornehmen. Dies würden wir machen, indem wir die Reparaturfunktion rekursiv auf dem Großelternknoten aufrufen.
Fall 4: Elternknoten ist rot, Onkelknoten ist schwarz, eingefügter Knoten ist "innerer Enkel"
Diesen Fall muss ich zunächst erklären: "innerer Enkel" bedeutet, dass der Weg vom Großeltern-Knoten zum eingefügten Knoten ein Dreieck bildet, wie in folgender Grafik anhand der 19, 75 und 24 gezeigt. In diesem Beispiel sieht man außerdem, dass auch ein NIL-Blatt als schwarzer Onkelknoten angesehen wird (entsprechend Regel 3).
(Die jeweils zwei NIL-Blätter der 9 und der 24, sowie das rechte NIL-Blatt der 75 habe ich der Übersicht halber nicht mit eingezeichnet.)

In diesem Fall rotieren wir zunächst am Elternknoten in entgegengesetzter Richtung des eingefügten Knotens.
Was bedeutet das?
Wenn der eingefügte Knoten linkes Kind seines Elternknotens ist, rotieren wir am Elternknoten nach rechts. Wenn der eingefügte Knoten rechtes Kind ist, dann rotieren wir nach links.
Im Beispiel ist der eingefügte Knoten (die 24) linkes Kind, also rotieren wir am Elternknoten (im Beispiel 75) nach rechts:

Als zweites rotieren wir am Großelternknoten in entgegengesetzter Richtung zur vorherigen Rotation (im Beispiel an der 19 linksherum):
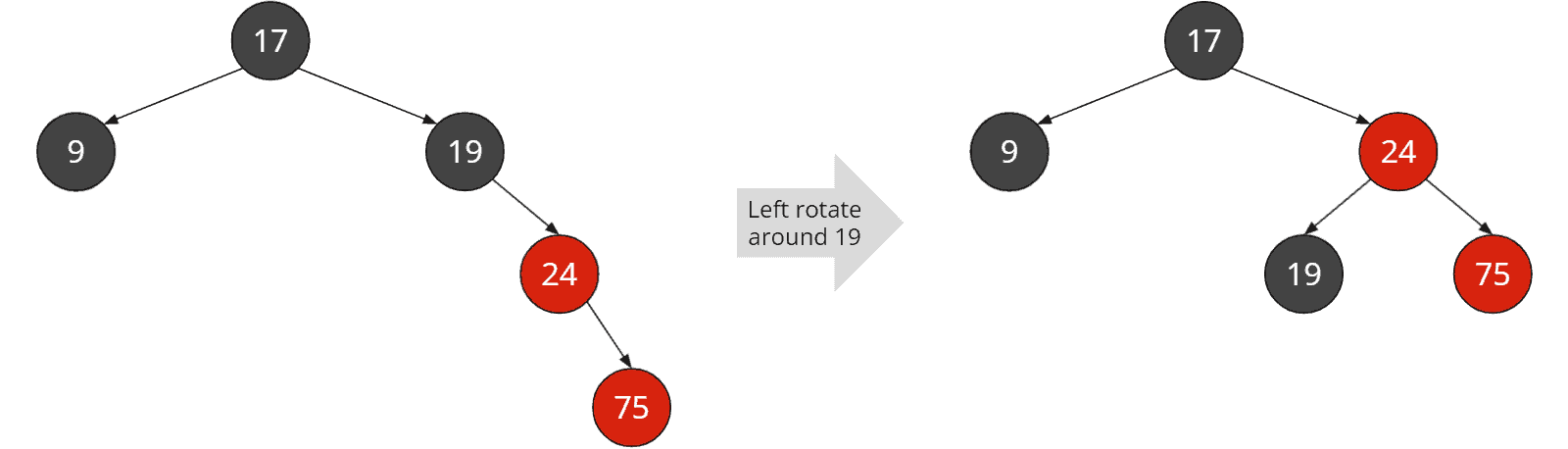
Zuletzt färben wir den gerade eingefügten Knoten (im Beispiel die 24) schwarz und den ursprünglichen Großelternknoten (im Beispiel die 19) rot:

Da an der Spitze des zuletzt rotierten Teilbaumes jetzt ein schwarzer Knoten steht, kann es dort nicht zu einer Verletzung von Regel 4 ("kein rot-rot!") kommen.
Auch das Rotfärben des ursprünglichen Großelternknotens (19) kann nicht zu einer Verletzung von Regel 4 führen. Denn dessen linkes Kind ist der Onkelknoten, der per Definition dieses Falles schwarz ist. Und das rechte Kind ist als Folge der zweiten Rotation das linke Kind des eingefügten Knotens, also ein schwarzes NIL-Blatt.
Die eingefügte rote 75 hat als Kinder zwei NIL-Blätter, somit gibt es auch hier keinen Verstoß gegen Regel 4.
Die Reparatur ist damit abgeschlossen, ein rekursiver Aufruf der Reparaturfunktion ist nicht erforderlich.
Fall 5: Elternknoten ist rot, Onkelknoten ist schwarz, eingefügter Knoten ist "äußerer Enkel"
"Äußerer Enkel" bedeutet, dass der Weg vom Großelternknoten zum eingefügten Knoten eine Linie bildet, wie in folgendem Beispiel die 19, die 75 und die gerade eingefügte 81:

In diesem Fall rotieren wir am Großelternknoten (im Beispiel 19) in entgegengesetzter Richtung des Eltern- und eingefügten Knotens (beide gehen in diesem Fall ja in die gleiche Richtung). Im Beispiel sind Eltern- und eingefügter Knoten jeweils rechtes Kind, also rotieren wir am Großelternknoten nach links:

Danach färben wir den ehemaligen Elternknoten (im Beispiel die 75) schwarz und den ehemaligen Großelternknoten (die 19) rot:

Wie am Ende von Fall 4 haben wir an der Spitze der Rotation einen schwarzen Knoten, so dass es dort zu keiner Verletzung von Regel 4 ("kein rot-rot!") kommen kann.
Das linke Kind der 19 ist nach der Rotation der ursprüngliche Onkelknoten, also per Fall-Definition schwarz; das rechte Kind der 19 ist das ursprünglich linke Kind des Elternknotens (75), welches ebenfalls ein schwarzes NIL-Blatt sein muss, da sonst der rechte Platz, an dem wir die 81 eingefügt haben, nicht frei gewesen wäre (denn ein roter Knoten hat immer entweder zwei schwarze Kinder mit Wert oder zwei schwarze NIL-Kinder).
Die rote 81 ist der eingefügte Knoten und hat daher ebenfalls zwei schwarze NIL-Blätter.
Die Reparatur des Rot-Schwarz-Baumes ist an dieser Stelle abgeschlossen.
Wer genau aufgepasst hat, stellt fest: Fall 5 entspricht exakt der zweiten Rotation aus Fall 4. Im Code wird sich das dadurch zeigen, dass für Fall 4 nur die erste Rotation implementiert ist und danach zum Code von Fall 5 gesprungen wird.
Implementierung der Reparaturfunktion nach dem Einfügen
Die vollständige Reparaturfunktion findest du in RedBlackTree ab Zeile 64. Die Fälle 1 bis 5 sind durch Kommentare markiert. Die Fälle 4 und 5 sind in 4a/4b und 5a/5b aufgeteilt, je nachdem, ob der Elternknoten linkes (4a/5a) oder rechtes Kind (4b/5b) des Großelternknotens ist.
private void fixRedBlackPropertiesAfterInsert(Node node) {
Node parent = node.parent;
// Case 1: Parent is null, we've reached the root, the end of the recursion
if (parent == null) {
// Uncomment the following line if you want to enforce black roots (rule 2):
// node.color = BLACK;
return;
}
// Parent is black --> nothing to do
if (parent.color == BLACK) {
return;
}
// From here on, parent is red
Node grandparent = parent.parent;
// Case 2:
// Not having a grandparent means that parent is the root. If we enforce black roots
// (rule 2), grandparent will never be null, and the following if-then block can be
// removed.
if (grandparent == null) {
// As this method is only called on red nodes (either on newly inserted ones - or -
// recursively on red grandparents), all we have to do is to recolor the root black.
parent.color = BLACK;
return;
}
// Get the uncle (may be null/nil, in which case its color is BLACK)
Node uncle = getUncle(parent);
// Case 3: Uncle is red -> recolor parent, grandparent and uncle
if (uncle != null && uncle.color == RED) {
parent.color = BLACK;
grandparent.color = RED;
uncle.color = BLACK;
// Call recursively for grandparent, which is now red.
// It might be root or have a red parent, in which case we need to fix more...
fixRedBlackPropertiesAfterInsert(grandparent);
}
// Parent is left child of grandparent
else if (parent == grandparent.left) {
// Case 4a: Uncle is black and node is left->right "inner child" of its grandparent
if (node == parent.right) {
rotateLeft(parent);
// Let "parent" point to the new root node of the rotated sub-tree.
// It will be recolored in the next step, which we're going to fall-through to.
parent = node;
}
// Case 5a: Uncle is black and node is left->left "outer child" of its grandparent
rotateRight(grandparent);
// Recolor original parent and grandparent
parent.color = BLACK;
grandparent.color = RED;
}
// Parent is right child of grandparent
else {
// Case 4b: Uncle is black and node is right->left "inner child" of its grandparent
if (node == parent.left) {
rotateRight(parent);
// Let "parent" point to the new root node of the rotated sub-tree.
// It will be recolored in the next step, which we're going to fall-through to.
parent = node;
}
// Case 5b: Uncle is black and node is right->right "outer child" of its grandparent
rotateLeft(grandparent);
// Recolor original parent and grandparent
parent.color = BLACK;
grandparent.color = RED;
}
}
Code-Sprache: Java (java)Die Hilfsfunktion getUncle() findest du ab Zeile 152:
private Node getUncle(Node parent) {
Node grandparent = parent.parent;
if (grandparent.left == parent) {
return grandparent.right;
} else if (grandparent.right == parent) {
return grandparent.left;
} else {
throw new IllegalStateException("Parent is not a child of its grandparent");
}
}Code-Sprache: Java (java)Anmerkungen zur Implementierung
Im Gegensatz zum AVL-Baum können wir die Reparatur-Funktion des Rot-Schwarz-Baumes nicht ohne weiteres in die bestehende Rekursion aus BinarySearchTreeRecursive einhängen. Der Grund dafür ist, dass wir nicht nur an demjenigen Knoten rotieren müssen, unter dem wir den neuen Knoten eingefügt haben, sondern ggf. auch am Großelternknoten (Fälle 3 und 4).
Du wirst in der Literatur zahlreiche alternative Implementierungen finden. Diese sind teilweise minimal performanter als der hier vorgestellte Weg, da mehrere Schritte kombiniert werden. Das ändert nichts an der Größenordnung der Performance, kann aber ein paar Prozente herausholen. Mir war es in erster Linie wichtig den Algorithmus verständlich zu implementieren. Die performanteren Algorithmen sind immer auch komplexer.
Ich habe das iterative Einfügen hier in zwei Schritten implementiert – erst Suche, dann Einfügen – im Gegensatz zu BinarySearchTreeIterative, wo beides kombiniert war. Das macht das Lesen etwas einfacher, benötigt allerdings auch einen zusätzlichen "if (key < parent.data)"-Check, um zu bestimmen, ob der neue Knoten als linkes oder rechtes Kind unter seinen Elternknoten eingefügt werden muss.
Löschen aus einem Rot-Schwarz-Baum
Wenn du das Kapitel über das Einfügen gerade fertiggelesen hast, solltest du vielleicht eine kurze Pause machen. Denn das Löschen ist noch komplexer.
Zunächst gehen wir so vor, wie im Abschnitt "Löschen im binären Suchbaum" des Artikels über binäre Suchbäume im Allgemeinen beschrieben.
Hier noch einmal eine kurze Zusammenfassung:
- Hat der zu löschende Knoten keine Kinder, entfernen wir ihn einfach.
- Hat der zu löschende Knoten ein Kind, dann entfernen wir den Knoten und lassen sein einziges Kind an dessen Position aufrücken.
- Hat der zu löschende Knoten zwei Kinder, dann kopieren wir den Inhalt (nicht die Farbe!) des In-Order-Nachfolgers des rechten Kindes in den zu löschenden Knoten und löschen danach den In-Order-Nachfolger nach Vorschrift 1 oder 2 (der In-Order-Nachfolger hat per Definiton maximal ein Kind).
Danach müssen wir die Regeln des Baumes überprüfen und ggf. den Baum reparieren. Dazu müssen wir uns merken, welche Farbe der gelöschte Knoten hat und welchen Knoten wir haben aufrücken lassen.
- Ist der gelöschte Knoten rot, dann können wir keine Regel verletzt haben: Weder kann es dadurch zu zwei aufeinanderfolgenden roten Knoten kommen (Regel 4), noch ändert sich die Anzahl schwarzer Knoten auf irgendeinem Pfad (Regel 5).
- Ist der gelöschte Knoten allerdings schwarz, haben wir Regel 5 garantiert verletzt (außer der Baum enthielt nichts als eine schwarze Wurzel) und Regel 4 möglicherweise auch – nämlich dann, wenn sowohl Elternknoten als auch das aufgerückte Kind des gelöschten Knotens rot waren.
Hier zunächst der Code für das eigentliche Löschen eines Knotens (Klasse RedBlackTree, Zeile 163). Unter dem Code erkläre ich dir dessen Teile:
public void deleteNode(int key) {
Node node = root;
// Find the node to be deleted
while (node != null && node.data != key) {
// Traverse the tree to the left or right depending on the key
if (key < node.data) {
node = node.left;
} else {
node = node.right;
}
}
// Node not found?
if (node == null) {
return;
}
// At this point, "node" is the node to be deleted
// In this variable, we'll store the node at which we're going to start to fix the R-B
// properties after deleting a node.
Node movedUpNode;
boolean deletedNodeColor;
// Node has zero or one child
if (node.left == null || node.right == null) {
movedUpNode = deleteNodeWithZeroOrOneChild(node);
deletedNodeColor = node.color;
}
// Node has two children
else {
// Find minimum node of right subtree ("inorder successor" of current node)
Node inOrderSuccessor = findMinimum(node.right);
// Copy inorder successor's data to current node (keep its color!)
node.data = inOrderSuccessor.data;
// Delete inorder successor just as we would delete a node with 0 or 1 child
movedUpNode = deleteNodeWithZeroOrOneChild(inOrderSuccessor);
deletedNodeColor = inOrderSuccessor.color;
}
if (deletedNodeColor == BLACK) {
fixRedBlackPropertiesAfterDelete(movedUpNode);
// Remove the temporary NIL node
if (movedUpNode.getClass() == NilNode.class) {
replaceParentsChild(movedUpNode.parent, movedUpNode, null);
}
}
}Code-Sprache: Java (java)Die ersten Zeilen des Codes suchen den zu löschenden Knoten; wird dieser nicht gefunden, wird die Methode beendet.
Wie es weiter geht, hängt von der Anzahl der Kinder zu löschenden Knotens ab.
Löschen eines Knotens mit keinem oder einem Kind
Hat der gelöschte Knoten maximal ein Kind, wird die Methode deleteNodeWithZeroOrOneChild() aufgerufen. Diese findest du im Quellcode ab Zeile 221:
private Node deleteNodeWithZeroOrOneChild(Node node) {
// Node has ONLY a left child --> replace by its left child
if (node.left != null) {
replaceParentsChild(node.parent, node, node.left);
return node.left; // moved-up node
}
// Node has ONLY a right child --> replace by its right child
else if (node.right != null) {
replaceParentsChild(node.parent, node, node.right);
return node.right; // moved-up node
}
// Node has no children -->
// * node is red --> just remove it
// * node is black --> replace it by a temporary NIL node (needed to fix the R-B rules)
else {
Node newChild = node.color == BLACK ? new NilNode() : null;
replaceParentsChild(node.parent, node, newChild);
return newChild;
}
}
Code-Sprache: Java (java)Die hier mehrfach aufgerufene Methode replaceParentsChild() habe ich dir bereits bei der Rotation vorgestellt.
Der Fall, dass der gelöschte Knoten schwarz ist und keine Kinder hat, stellt eine Besonderheit dar. Dieser wird im letzten else-Block behandelt:
Wir haben oben festgestellt, dass das Löschen eines schwarzen Knotens dazu führt, dass die Anzahl schwarzer Knoten nicht mehr auf allen Pfaden gleich ist. D. h., wir werden den Baum reparieren müssen. Die Baumreparatur beginnt (wie du in Kürze sehen wirst) immer beim aufgerückten Knoten.
Wenn der gelöschte Knoten keine Kinder hat, rückt quasi eines seiner NIL-Blätter an seine Position auf. Um später von diesem NIL-Blatt zu seinem Elternknoten navigieren zu können, brauchen wir einen speziellen Platzhalter. Dieser ist in der Klasse NilNode implementiert, die du im Quellcode ab Zeile 349 findest:
private static class NilNode extends Node {
private NilNode() {
super(0);
this.color = BLACK;
}
}Code-Sprache: Java (java)Die Methode deleteNodeWithZeroOrOneChild() gibt schließlich den aufgerückten Knoten zurück, den sich die aufrufende Methode deleteNode() in der Variablen movedUpNode merkt.
Löschen eines Knotens mit zwei Kindern
Hat der zu löschende Knoten zwei Kinder, suchen wir zunächst mit der Methode findMinimum() (Zeile 244) den In-Order-Nachfolger des Teilbaumes, der am rechten Kind beginnt:
private Node findMinimum(Node node) {
while (node.left != null) {
node = node.left;
}
return node;
}Code-Sprache: Java (java)Daraufhin kopieren wir die Daten des In-Order-Nachfolgers in den zu löschenden Knoten und rufen die oben vorgestellte Methode deleteNodeWithZeroOrOneChild() auf, um den In-Order-Nachfolger aus dem Baum zu entfernen. Wiederum merken wir uns den aufgerückten Knoten in movedUpNode.
Reparatur des Baumes
Hier noch einmal der letzte if-Block der deleteNode()-Methode:
if (deletedNodeColor == BLACK) {
fixRedBlackPropertiesAfterDelete(movedUpNode);
// Remove the temporary NIL node
if (movedUpNode.getClass() == NilNode.class) {
replaceParentsChild(movedUpNode.parent, movedUpNode, null);
}
}Code-Sprache: Java (java)Wie oben bereits festgestellt, werden durch das Löschen eines roten Knotens keine Regeln verletzt. Wenn der gelöschte Knoten hingegen schwarz ist, rufen wir die Reparaturmethode fixRedBlackPropertiesAfterDelete() auf.
Der ggf. in deleteNodeWithZeroOrOneChild() angelegte temporäre NilNode-Platzhalter wurde nur für den Aufruf der Reparaturfunktion benötigt und kann daher im Anschluss entfernt werden.
Beim Löschen müssen wir noch einen Fall mehr beachten als beim Einfügen: nämlich sechs. Im Gegensatz zum Einfügen ist dabei nicht die Farbe des Onkelknotens relevant, sondern die des Geschwisterknotens des aufgerückten Knotens.
- Fall 1: Aufgerückter Knoten ist die Wurzel
- Fall 2: Geschwisterknoten ist rot
- Fall 3: Geschwisterknoten ist schwarz und hat zwei schwarze Kinder, Elternknoten ist rot
- Fall 4: Geschwisterknoten ist schwarz und hat zwei schwarze Kinder, Elternknoten ist schwarz
- Fall 5: Geschwisterknoten ist schwarz und hat mind. ein rotes Kind, "äußerer Neffe" ist schwarz
- Fall 6: Geschwisterknoten ist schwarz und hat mind. ein rotes Kind, "äußerer Neffe" ist rot
Die folgenden Abschnitte beschreiben die sechs Fälle im Detail:
Fall 1: Aufgerückter Knoten ist die Wurzel
Wurde die Wurzel entfernt, rückt ein anderer Knoten an deren Position auf. Das kann nur dann passieren, wenn die Wurzel kein oder nur ein Kind hatte. Denn hätte die Wurzel zwei Kinder gehabt, wäre letztendlich der In-Order-Nachfolger entfernt worden und nicht der Wurzelknoten.
Wenn die Wurzel kein Kind hatte, ist die neue Wurzel ein schwarzer NIL-Knoten. Somit ist der Baum leer und gültig:

Wenn die Wurzel ein Kind hatte, dann musste dies rot sein und keine weiteren Kinder haben.
Denn: Hätte das rote Kind ein weiteres rotes Kind, wäre Regel 4 ("kein rot-rot!") verletzt gewesen. Hätte das rote Kind ein schwarzes Kind, dann hätten die Pfade durch den roten Knoten wenigstens einen schwarzen Knoten mehr als der NIL-Teilbaum der Wurzel, und damit wäre Regel 5 verletzt gewesen.
Somit besteht der Baum nur noch aus einer roten Wurzel und ist damit ebenfalls gültig.

Sollten wir mit Regel 2 arbeiten ("die Wurzel ist immer schwarz"), dann würden wir an dieser Stelle die Wurzel schwarz färben.
Fall 2: Geschwisterknoten ist rot
Für alle anderen Fälle prüfen wir zunächst die Farbe des Geschwisterknotens. Dies ist das zweite Kind des Elternknotens des gelöschten Knotens. In folgendem Beispiel löschen wir die 9; deren Geschwisterknoten ist die rote 19:

In diesem Fall färben wir zunächst den Geschwisterknoten schwarz und den Elternknoten rot:

Dadurch wurde offensichtlich Regel 5 verletzt: Die Pfade im rechten Teilbaum des Elternknotens haben jeweils zwei schwarze Knoten mehr als die des linken Teilbaum. Dies beheben wir durch eine Rotation um den Elternknoten in Richtung des gelöschten Knotens.
Im Beispiel haben wir den linken Knoten des Elternknotens gelöscht – wir führen daher eine Links-Rotation durch:

Jetzt haben wir auf dem rechten Pfad zwei schwarze Knoten, auf dem zur 18 ebenfalls zwei. Allerdings haben wir nur einen schwarzen Knoten auf dem Pfad zum linken NIL-Blatt der 17 (zur Erinnerung: die Wurzel zählt nicht mit, die NIL-Knoten zählen mit – auch die in der Grafik nicht eingezeichneten).
Wir schauen auf den neuen Geschwisterknoten des gelöschten Knotens (im Beispiel die 18). Dieser ist jetzt in jedem Fall schwarz, denn es handelt sich um ein ursprüngliches Kind des roten Geschwisterknotens vom Anfang des Falls.
Außerdem hat der neue Geschwisterknoten schwarze Kinder. Deshalb färben wir den Geschwisterknoten (die 18) rot und den Elternknoten (die 17) schwarz:

Jetzt haben alle Pfade zwei schwarze Knoten; wir haben also wieder einen gültigen Rot-Schwarz-Baum.
Fall 2 ‒ Fall-Through
Tatsächlich habe ich in diesem letzten Schritt etwas vorweggenommen. Wir haben nämlich die Regeln von Fall 3 ausgeführt (deswegen ist der Bilduntertitel auch in Klammern).
In diesem letzten Schritt von Fall 2 haben wir immer einen schwarzen Geschwisterknoten. Dass dieser zwei schwarze Kinder hatte, wie für Fall 3 gefordert, war Zufall. Tatsächlich kann am Ende von Fall 2 jeder der Fälle 3 bis 6 eintreten und muss entsprechend der folgenden Abschnitte behandelt werden.
Fall 3: Geschwisterknoten ist schwarz und hat zwei schwarze Kinder, Elternknoten ist rot
In folgendem Beispiel löschen wir die 75 und lassen eines seiner schwarzen NIL-Blätter aufrücken.
(Nochmal zur Erinnerung: Ich zeige in den Grafiken nur dann NIL-Blätter an, wenn diese für das Verständnis relevant sind.)

Das führt zu einem Verstoß von Regel 5: Im ganz rechten Pfad haben wir jetzt einen schwarzen Knoten weniger als in allen anderen.
Der Geschwisterknoten (im Beispiel die 18) ist schwarz und hat zwei schwarze Kinder (die nicht dargestellten NIL-Blätter). Der Elternknoten (die 19) ist rot. In diesem Fall reparieren wir den Baum wie folgt:
Wir färben den Geschwisterknoten (die 18) rot und den Elternknoten (die 19) schwarz:

Somit haben wir wieder einen gültigen Rot-Schwarz-Baum. Die Anzahl der schwarzen Knoten ist auf allen Pfaden gleich (wie von Regel 5 gefordert). Und da der Geschwisterknoten nur schwarze Kinder hat, kann es durch das Rotfärben desselben nicht zu einer Verletzung von Regel 4 ("kein rot-rot!") kommen.
Fall 4: Geschwisterknoten ist schwarz und hat zwei schwarze Kinder, Elternknoten ist schwarz
Im nächsten Beispiel löschen wir die 18:

Dies führt (genau wie bei Fall 3) zu einem Verstoß gegen Regel 5: Auf dem Pfad zum gelöschten Knoten haben wir jetzt einen schwarzen Knoten weniger als auf allen anderen Pfaden.
Im Gegensatz zu Fall 3 ist bei Fall 4 der Elternknoten des gelöschten Knotens schwarz. Wir färben zunächst den Geschwisterknoten rot:

Damit ist die Schwarzhöhe in demjenigen Teilbaum, der am Elternknoten beginnt, wieder einheitlich (nämlich 2). Im linken Teilbaum ist sie allerdings eins höher (3). Gegen Regel 5 wird also noch immer verstoßen.
Fall 4 ‒ Rekursion
Dieses Problem lösen wir, indem wir so tun, als hätten wir zwischen der 17 und der 19 einen schwarzen Knoten gelöscht (was den gleichen Effekt gehabt hätte). Dementsprechend rufen wir die Reparaturfunktion rekursiv auf dem Elternknoten, also der 19 auf (was in diesem Fall der aufgerückte Knoten gewesen wäre).
Die 19 hat einen schwarzen Geschwisterknoten (die 9) mit zwei schwarzen Kindern (3 und 12) und einem roten Elternteil (17). Dementsprechend sind wir jetzt wieder bei Fall 3.
Fall 3 lösen wir, in dem wir den Geschwisterknoten rot und den Elternknoten schwarz färben:

Die Schwarzhöhe beträgt nun auf allen Pfaden 2. Unser Rot-Schwarz-Baum ist damit wieder valide.
Fall 5: Geschwisterknoten ist schwarz und hat mindestens ein rotes Kind, "äußerer Neffe" ist schwarz
In diesem Beispiel löschen wir die 18:

Als Folge haben wir wieder einen Verstoß gegen Regel 5, da der Teilbaum, der am Geschwisterknoten beginnt, jetzt eine um eins größere Schwarzhöhe hat.
Wir betrachten den "äußeren Neffen" des gelöschten Knotens. "Äußerer Neffe" bezeichnet dasjenige Kind des Geschwisterknotens, das gegenüber dem gelöschten Knoten liegt. Im Beispiel ist das das rechte, per Definition schwarze, NIL-Blatt unter der 75.
In folgender Grafik siehst du, dass Elternknoten, Geschwisterknoten und Neffe gemeinsam eine Linie bilden (im Beispiel die 19, die 75 und dessen rechtes NIL-Kind).
Wir beginnen mit der Reparatur, indem wir den inneren Neffen (im Beispiel die 24) schwarz färben und den Geschwisterknoten (die 75) rot:

Danach führen wir eine Rotation am Geschwisterknoten in entgegengesetzter Richtung des gelöschten Knotens durch. Im Beispiel wurde das linke Kind des Elternknotens gelöscht, also erfolgt am Geschwisterknoten (der 75) eine Rotation nach rechts:

Wir führen erneut ein paar Umfärbungen durch:
- Wir färben den Geschwisterknoten in der Farbe des Elternknotens (im Beispiel die 24 rot).
- Dann färben wir den Elternknoten (die 19) sowie den äußeren Neffen des gelöschten Knotens, also das rechte Kind des neuen Geschwisterknotens (im Beispiel die 75) schwarz:

Als letztes führen wir eine Rotation am Elternknoten in Richtung des gelöschten Knotens durch. Im Beispiel war der gelöschte Knoten das linke Kind, dementsprechend führen wir eine Links-Rotation aus (im Beispiel an der 19):

Damit werden alle Rot-Schwarz-Regeln wieder eingehalten. Es gibt keine zwei aufeinanderfolgenden roten Knoten, und die Anzahl schwarzer Knoten beträgt auf allen Pfaden einheitlich zwei. Die Reparatur des Baumes ist damit abgeschlossen.
Fall 6: Geschwisterknoten ist schwarz und hat mindestens ein rotes Kind, "äußerer Neffe" ist rot
Im letzten Beispiel, welches Fall 5 stark ähnelt, löschen wir ebenfalls die 18:

Als Folge haben wir, wie in Fall 5, einen Verstoß gegen Regel 5, da der Pfad zum gelöschten Knoten nun einen schwarzen Knoten weniger enthält.
Bei Fall 6 ist, im Gegensatz zu Fall 5, der äußere Neffe (im Beispiel die 81) rot und nicht schwarz.
Wir färben zunächst den Geschwisterknoten in der Farbe des Elternknotens (im Beispiel die 75 rot). Danach färben wir den Elternknoten (im Beispiel die 19) und den äußeren Neffen (die 81) schwarz:
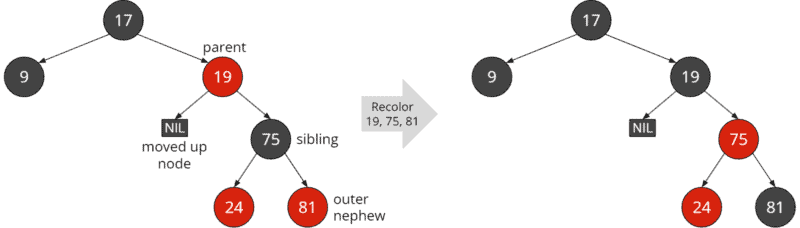
Als zweites führen wir am Elternknoten eine Rotation in Richtung des gelöschten Knotens durch. Im Beispiel wurde das linke Kind seines Elternknotens gelöscht; entsprechend vollziehen wir eine Links-Rotation um die 19:

Damit sind die Rot-Schwarz-Regeln wiederhergestellt. Es folgen keine zwei roten Knoten aufeinander, und die Anzahl der schwarzen Knoten ist auf allen Pfaden gleich (nämlich 2).
Die Vorschriften in diesem letzten Fall gleichen den letzten zwei Schritten aus Fall 5. Im Quellcode wirst du sehen, dass für Fall 5 nur dessen ersten zwei Schritte implementiert sind und die Ausführung dann zu Fall 6 springt, um die letzten zwei Schritte auszuführen.
Damit haben wir alle sechs Fälle betrachtet. Kommen wir zur Implementierung der Reparaturfunktion in Java.
Implementierung der Reparaturfunktion nach dem Löschen
Du findest die Reparaturmethode fixRedBlackPropertiesAfterDelete() im Quellcode ab Zeile 252. Die Fälle 1 bis 6 sind durch Kommentare markiert.
private void fixRedBlackPropertiesAfterDelete(Node node) {
// Case 1: Examined node is root, end of recursion
if (node == root) {
// Uncomment the following line if you want to enforce black roots (rule 2):
// node.color = BLACK;
return;
}
Node sibling = getSibling(node);
// Case 2: Red sibling
if (sibling.color == RED) {
handleRedSibling(node, sibling);
sibling = getSibling(node); // Get new sibling for fall-through to cases 3-6
}
// Cases 3+4: Black sibling with two black children
if (isBlack(sibling.left) && isBlack(sibling.right)) {
sibling.color = RED;
// Case 3: Black sibling with two black children + red parent
if (node.parent.color == RED) {
node.parent.color = BLACK;
}
// Case 4: Black sibling with two black children + black parent
else {
fixRedBlackPropertiesAfterDelete(node.parent);
}
}
// Case 5+6: Black sibling with at least one red child
else {
handleBlackSiblingWithAtLeastOneRedChild(node, sibling);
}
}Code-Sprache: Java (java)Die Hilfsmethoden getSibling() und isBlack() findest du ab Zeile 334:
private Node getSibling(Node node) {
Node parent = node.parent;
if (node == parent.left) {
return parent.right;
} else if (node == parent.right) {
return parent.left;
} else {
throw new IllegalStateException("Parent is not a child of its grandparent");
}
}
private boolean isBlack(Node node) {
return node == null || node.color == BLACK;
}Code-Sprache: Java (java)Ein roter Geschwisterknoten (Fall 2) wird ab Zeile 289 behandelt:
private void handleRedSibling(Node node, Node sibling) {
// Recolor...
sibling.color = BLACK;
node.parent.color = RED;
// ... and rotate
if (node == node.parent.left) {
rotateLeft(node.parent);
} else {
rotateRight(node.parent);
}
}Code-Sprache: Java (java)Die Implementierung für einen schwarzen Geschwisterknoten mit wenigstens einem roten Kind (Fälle 5 und 6) findest du ab Zeile 302:
private void handleBlackSiblingWithAtLeastOneRedChild(Node node, Node sibling) {
boolean nodeIsLeftChild = node == node.parent.left;
// Case 5: Black sibling with at least one red child + "outer nephew" is black
// --> Recolor sibling and its child, and rotate around sibling
if (nodeIsLeftChild && isBlack(sibling.right)) {
sibling.left.color = BLACK;
sibling.color = RED;
rotateRight(sibling);
sibling = node.parent.right;
} else if (!nodeIsLeftChild && isBlack(sibling.left)) {
sibling.right.color = BLACK;
sibling.color = RED;
rotateLeft(sibling);
sibling = node.parent.left;
}
// Fall-through to case 6...
// Case 6: Black sibling with at least one red child + "outer nephew" is red
// --> Recolor sibling + parent + sibling's child, and rotate around parent
sibling.color = node.parent.color;
node.parent.color = BLACK;
if (nodeIsLeftChild) {
sibling.right.color = BLACK;
rotateLeft(node.parent);
} else {
sibling.left.color = BLACK;
rotateRight(node.parent);
}
}Code-Sprache: Java (java)Genau wie für das Einfügen, wirst du auch für das Löschen in der Literatur zahlreiche alternative Vorgehensweisen finden. Ich habe mich bemüht den Code so zu strukturieren, dass du den Codefluss so gut wie möglich nachvollziehen kannst.
Traversierung durch den Rot-Schwarz-Baum
Wie jeden Binärbaum können wir auch den Rot-Schwarz-Baum in Pre-order-, Post-order-, In-order-, Reverse-in-order- und Level-order-Reihenfolge traversieren. Die Traversierung wird im Abschnitt "Binärbaum-Traversierung" des Einführungsartikels über Binärbäume beschrieben.
Dort findest du auch den entsprechenden Java-Quellcode, implementiert in den Klassen DepthFirstTraversal, DepthFirstTraversalIterative und DepthFirstTraversalRecursive.
Die Traversal-Methoden arbeiten auf dem BinaryTree-Interface. Da auch der RedBlackTree dieses Interface implementiert, können die Traversierungsmethoden ohne weiteres auch auf diesen angewendet werden.
Zeitkomplexität des Rot-Schwarz-Baums
Eine Einführung in das Thema der Zeitkomplexität und der O-Notation findest du in diesem Grundlagenartikel.
Den Aufwand für die Suche, das Einfügen und Löschen eines Knotens im Binärbaum können wir wie folgt bestimmen:
Aufwand für die Suche
Bei der Suche folgen wir einem Pfad von der Wurzel bis zum gesuchten Knoten (oder zu einem NIL-Blatt). Auf jeder Ebene führen wir einen Vergleich durch. Der Aufwand für den Vergleich ist konstant.
Der Aufwand für die Suche ist damit propertional zur Baumhöhe.
Wir bezeichnen mit n die Anzahl der Knoten des Baums. Wir haben im Abschnitt "Höhe des Rot-Schwarz-Baumes" erkannt, dass der längste Pfad maximal doppelt so lang ist wie der kürzeste Pfad. Hieraus folgt, dass die Höhe des Baumes durch O(log n) begrenzt ist.
Der formale Beweis dafür würde den Rahmen dieses Artikels sprengen. Du kannst den Beweis auf Wikipedia nachlesen.
Die Zeitkomplexität für die Suche im Rot-Schwarz-Baum beträgt somit: O(log n)
Aufwand für das Einfügen
Beim Einfügen führen wir zunächst eine Suche durch. Derem Aufwand haben wir soeben als O(log n) bestimmt.
Als nächstes fügen wir einen Knoten ein. Der Aufwand hierfür ist unabhängig von der Baumgröße konstant, also O(1).
Danach überprüfen wir die Rot-Schwarz-Regeln und stellen diese ggf. wieder her. Dies tun wir beginnend beim eingefügten Knoten aufsteigend bis zur Wurzel. Auf jeder Ebene führen wir eine oder mehrere der folgenden Operationen durch:
- Prüfung der Farbe des Elternknotens
- Bestimmung des Onkelknotens und Prüfung dessen Farbe
- Umfärbung von ein bis maximal drei Knoten
- Durchführung von ein oder zwei Rotationen
Jede dieser Operationen hat in sich einen konstanten Aufwand O(1). Der Gesamtaufwand für das Überprüfen und die Reparatur des Baumes ist in Summe also ebenfalls proportional zu dessen Höhe.
Die Zeitkomplexität für das Einfügen in den Rot-Schwarz-Baum beträgt also ebenfalls: O(log n)
Aufwand für das Löschen
Genau wie beim Einfügen suchen wir zunächst den zu löschenden Knoten mit Aufwand O(log n).
Auch der Aufwand für das Löschen an sich ist unabhängig von der Baumgröße, also konstant O(1).
Für das Prüfen der Regeln und die Reparatur des Baumes fallen – maximal einmal pro Ebene – eine oder mehrere der folgenden Operationen an:
- Prüfung der Farbe des gelöschten Knotens
- Bestimmung des Geschwisterknotens und Prüfung dessen Farbe
- Prüfung der Farben der Kinder des Geschwisterknotens
- Umfärben des Elternknoten
- Umfärben von Geschwisterknoten und ggf. einem seiner Kinder
- Durchführung von ein oder zwei Rotationen
Auch diese Operationen haben in sich alle einen konstanten Aufwand. Somit ist also auch der Gesamtaufwand für das Prüfen und Wiederherstellen der Regeln nach dem Löschen eines Knotens proportional zur Baumhöhe.
Die Zeitkomplexität für das Löschen aus dem Rot-Schwarz-Baum beträgt also ebenfalls: O(log n)
Rot-Schwarz-Baum im Vergleich mit anderen Datenstrukturen
Die folgenden Abschnitte beschreiben die Unterschiede, sowie die Vor- und Nachteile des Rot-Schwarz-Baumes gegenüber alternativen Datenstrukturen.
Rot-Schwarz-Baum vs. AVL-Baum
Der Rot-Schwarz-Baum sowie der AVL-Baum sind selbstbalancierende binäre Suchbäume.
Beim Rot-Schwarz-Baum ist der längste Pfad zur Wurzel maximal doppelt so lang wie der kürzeste Pfad zur Wurzel. Beim AVL-Baum hingegen unterscheidet sich die Tiefe keiner zwei Teilbäume um mehr als 1.
Im Rot-Schwarz-Baum wird die Balance durch die Farben der Knoten, ein Set von Regeln, und durch Rotationen und Umfärben der Knoten sichergestellt. Im AVL-Baum hingegen werden die Höhen der Teilbäume verglichen und bei Bedarf Rotationen durchgeführt.
Diese Unterschiede in den Eigenschaften der zwei Baumarten fünren zu folgenden Unterschieden bzgl. Performance und Speicherbedarf:
- Aufgrund der gleichmäßigeren Balancierung des AVL-Baums erfolgt die Suche in diesem in der Regel schneller als im Rot-Schwarz-Baum. Von der Größenordnung her liegen aber beide im Bereich O(log n).
- Auch für das Einfügen und Löschen beträgt die Zeitkomplexität in beiden Bäumen O(log n). Im direkten Vergleich ist allerdings der Rot-Schwarz-Baum schneller, da dieser seltener rebalanciert wird.
- Beide Bäume benötigen zusätzlichen Speicher: der AVL-Baum ein Byte pro Knoten für die Höhe des an einem Knoten beginnenden Teilbaums; der Rot-Schwarz-Baum ein Bit pro Knoten für die Farbinformation. In der Praxis macht dies selten einen Unterschied, da ein einzelnes Bit in der Regel mindestens ein Byte belegt.
Erwartet man viele Einfüge-/Löschoperationen, dann sollte man also eher einen Rot-Schwarz-Baum einsetzen. Geht man dagegen von mehr Suchoperationen aus, dann sollte die Wahl auf den AVL-Baum fallen.
Rot-Schwarz-Baum vs. Binärer Suchbaum
Der Rot-Schwarz-Baum ist eine konkrete Implementierung eines selbstbalancierenden binären Suchbaums. Jeder Rot-Schwarz-Baum ist also auch ein binärer Suchbaum.
Es gibt auch andere Arten von binären Suchbäumen, wie z. B. den oben genannten AVL-Baum – oder triviale nicht-balancierte Implementierungen. Somit ist also nicht jeder binäre Suchbaum auch ein Rot-Schwarz-Baum.
Fazit
In diesem Tutorial hast du gelernt, was ein Rot-Schwarz-Baum ist, welche Regeln in ihm gelten und wie diese Regeln nach dem Einfügen und Löschen von Knoten überprüft und ggf. wiederhergestellt werden. Außerdem habe ich dir eine möglichst einfach zu verstehende Java-Implementierung vorgestellt.
Im JDK werden Rot-Schwarz-Bäume in der TreeMap (hier der Quellcode auf GitHub) und bei Bucket Collisions in der HashMap (hier der Quellcode) eingesetzt.
Damit endet die Tutorial-Serie über Binärbäume.
Wenn ich dir helfen konnte Binärbäume im Allgemeinen, binäre Suchbäume, AVL-Bäume und – in diesem Artikel – Rot-Schwarz-Bäume besser zu verstehen, freue ich mich über einen Kommentar. Teile den Artikel auch gerne über einen der Share-Buttons am Ende.
Möchtest du informiert werden, wenn der nächste Artikel auf HappyCoders.eu veröffentlicht wird? Dann klicke hier, um dich in den HappyCoders-Verteiler einzutragen.
