

Dieser Artikel ist Teil der Serie „Sortieralgorithmen: Ultimate Guide“ und…
- erklärt die Funktionsweise von Bubble Sort,
- stellt den Quellcode von Bubble Sort vor,
- erklärt, wie man die Zeitkomplexität von Bubble Sort herleitet
- und prüft, ob die Performance der eigenen Implementierung dem entsprechend der Zeitkomplexität erwarteten Laufzeitverhalten entspricht.
Die Quellcodes aller Artikel dieser Serie findest du in meinem GitHub-Repository.
Bubble Sort Algorithmus
Bei Bubble Sort (auch: "Bubblesort") werden jeweils zwei aufeinanderfolgende Elemente miteinander verglichen und – wenn das linke Element größer ist als das rechte – werden diese vertauscht.
Diese Vergleichs- und Tauschoperationen führt man von links nach rechts über alle Elemente durch, so dass nach dem ersten Durchlauf das größte Element ganz rechts positioniert ist (besser gesagt: spätestens nach dem ersten Durchlauf – es kann auch schon vorher dort angekommen sein).
Diesen Prozess wiederholt man solange, bis es in einem Durchlauf zu keinem weiteren Vertauschen mehr kommt.
Bubble Sort Beispiel
Im folgenden zeige ich, wie man das Array [6, 2, 4, 9, 3, 7] mit Bubble Sort sortiert:
Vorbereitung
Wir teilen das Array gedanklich in einen linken, nicht sortierten, und einen rechten, sortierten Teil. Der rechte Teil ist zu Beginn leer:

Iteration 1
Wir vergleichen die ersten beiden Elemente, die 6 und die 2. Da die 6 kleiner ist, vertauschen wir die Elemente:

Nun vergleichen wir das zweite mit dem dritten Element, also die 6 mit der 4. Auch diese liegen in verkehrter Reihenfolge vor und werden vertauscht:
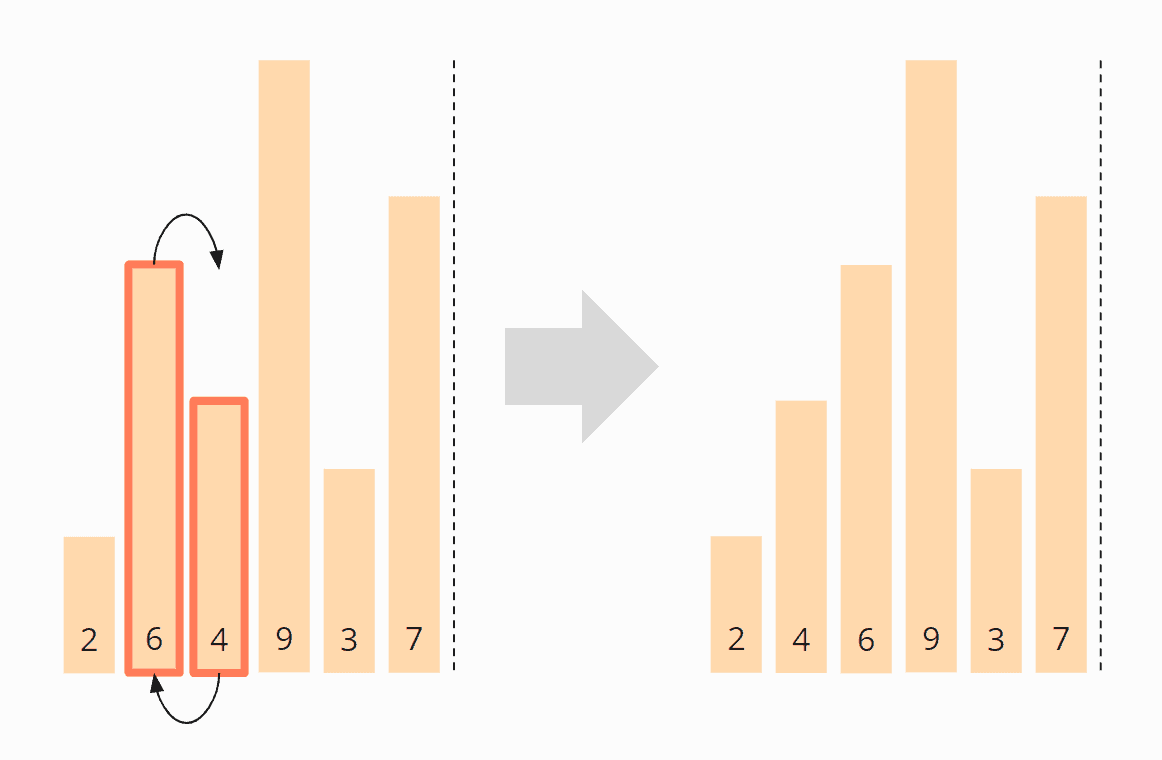
Wir vergleichen das dritte mit dem vierten Element, also die 6 mit der 9. Die 6 ist kleiner als die 9, also brauchen wir diese zwei Elemente nicht zu vertauschen.
Das vierte und fünfte Element, die 9 und die 3, müssen wiederum vertauscht werden:
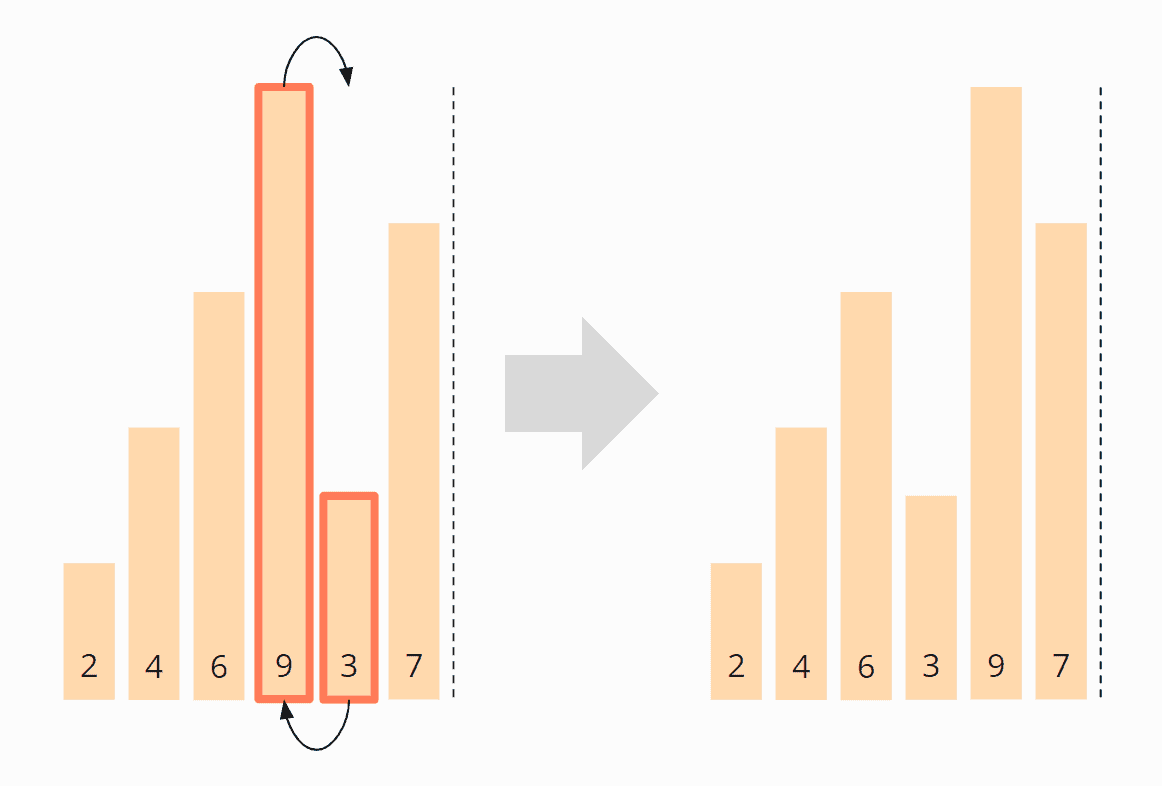
Und zuletzt müssen das fünfte und sechste Elemente, die 9 und die 7, miteinander vertauscht werden. Danach ist die erste Iteration abgeschlossen.

Die 9 hat ihre finale Position erreicht und wir verschieben die Grenze zwischen den Bereichen um eine Position nach links:

Diese Bereichsgrenze zeigt uns in der nächsten Iteration, bis zu welcher Position die Elemente vergleichen werden müssen. Die Bereichsgrenze gibt es übrigens nur in der optimierten Variante von Bubble Sort. In der ursprünglichen Variante fehlt sie, so dass in jeder Iteration unnötigerweise bis zum Ende des Arrays verglichen wird.
Iteration 2
Wir starten erneut am Anfang des Arrays und vergleichen die 2 mit der 4. Diese liegen in korrekter Reihenfolge vor und müssen nicht vertauscht werden.
Das gleiche gilt für die 4 und die 6.
Die 6 und die 3 hingegen müssen vertauscht werden, um in richtiger Reihenfolge vorzuliegen:
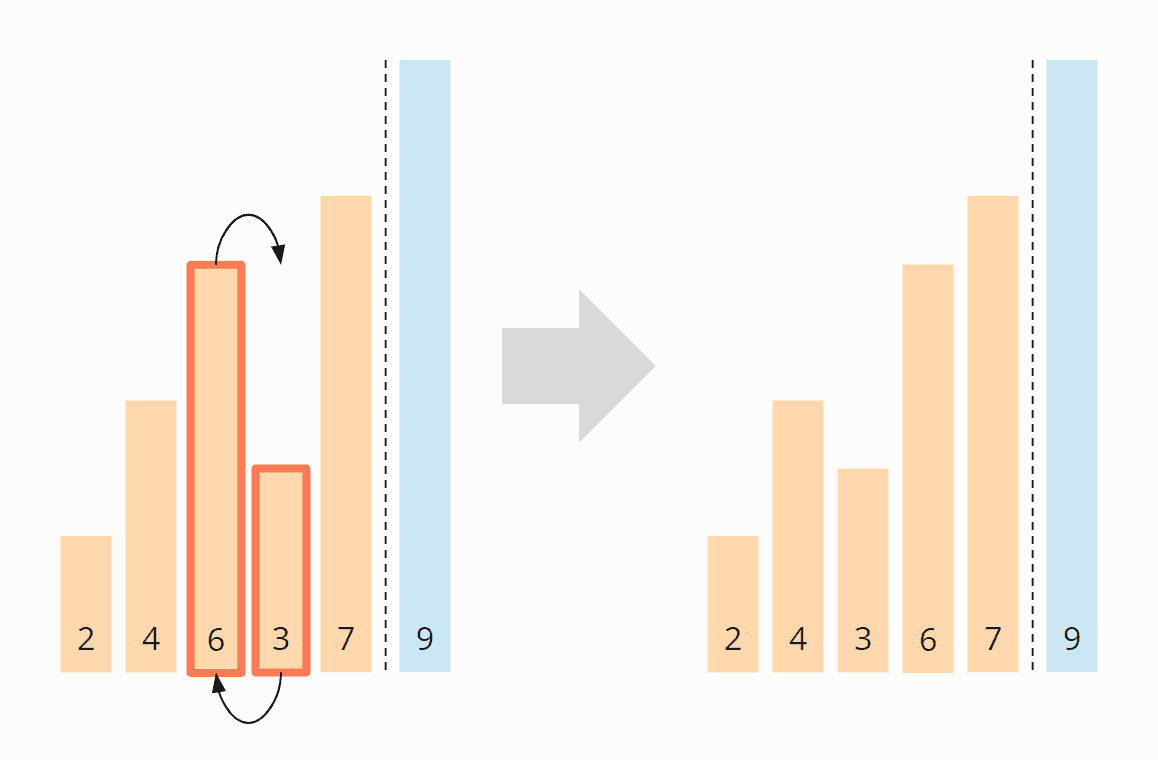
Die 6 und die 7 liegen in korrekter Reihenfolge vor und müssen nicht vertauscht werden. Weiter brauchen wir nicht zu vergleichen, denn die 9 liegt bereits im sortierten Bereich.
Zuletzt schieben wir die Bereichsgrenze wieder um eine Position nach links, damit wir die letzten zwei Elemente, die 7 und die 9, nicht weiter betrachten müssen.
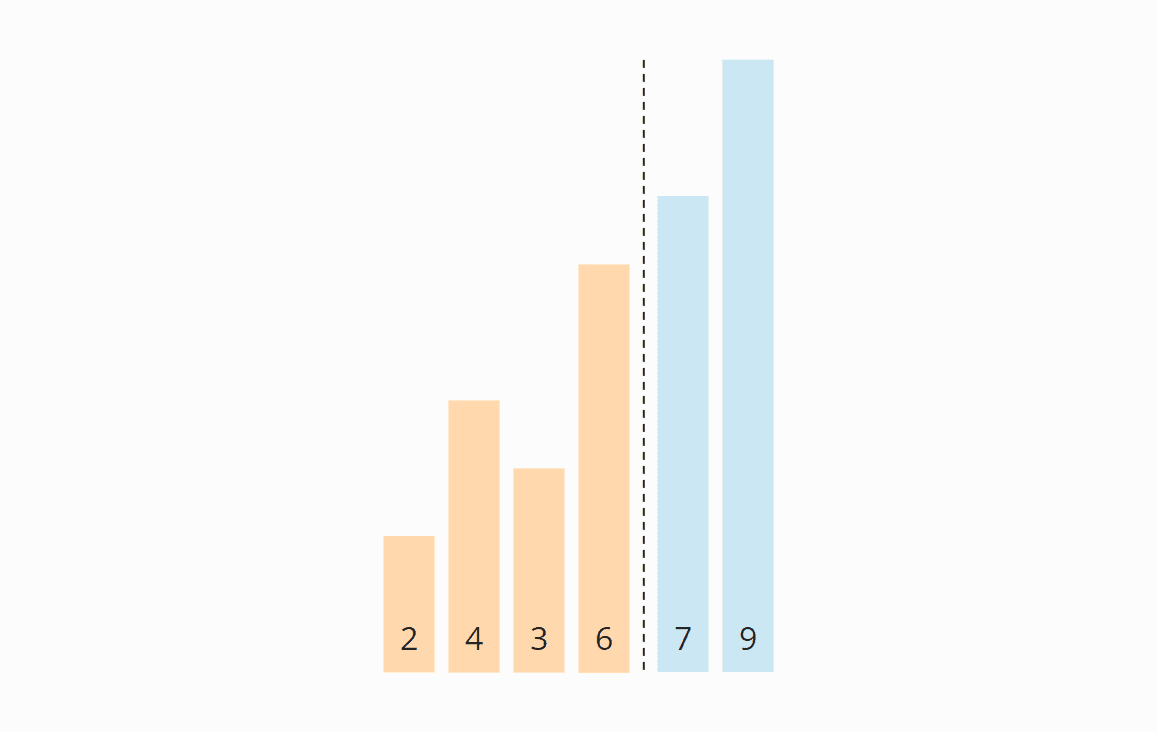
Iteration 3
Wieder starten wir am Anfang des Arrays. Die 2 und die 4 stehen korrekt zueinander. Die 4 und die 3 müssen vertauscht werden:
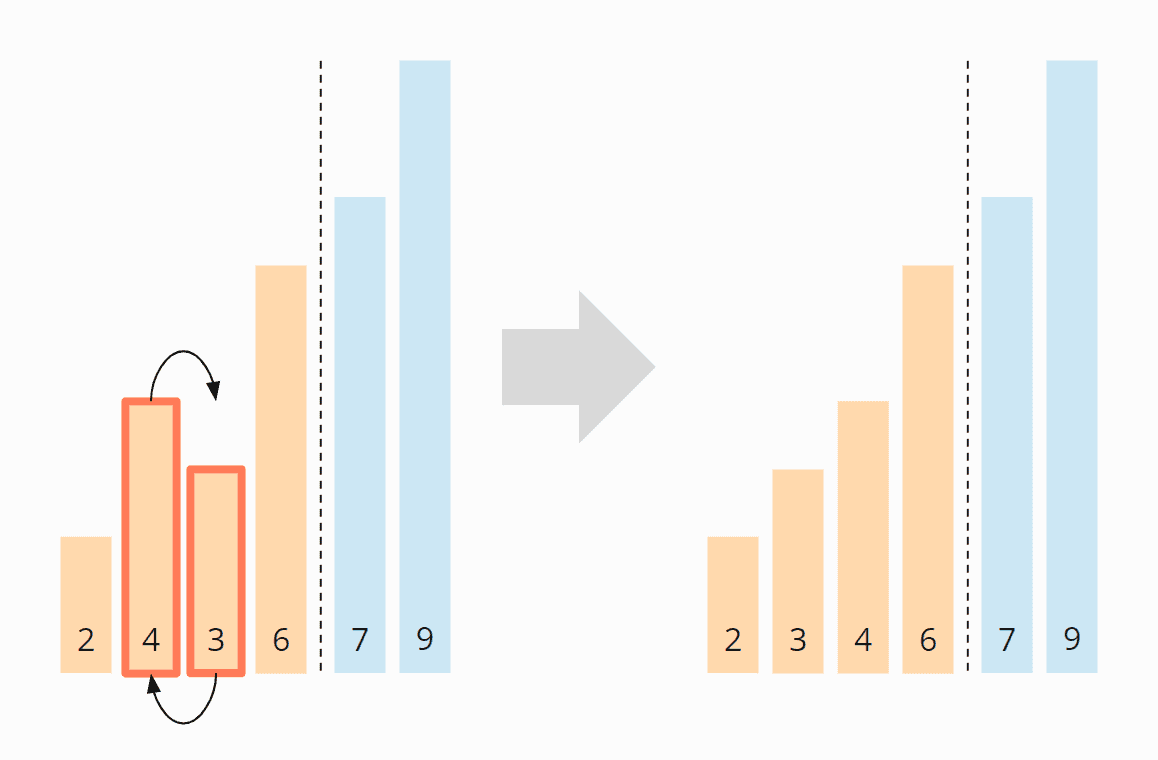
Die 4 und die 6 müssen nicht vertauscht werden. Die 7 und die 9 sind bereits sortiert. Damit ist diese Iteration auch schon beendet und wir schieben die Bereichsgrenze nach links:
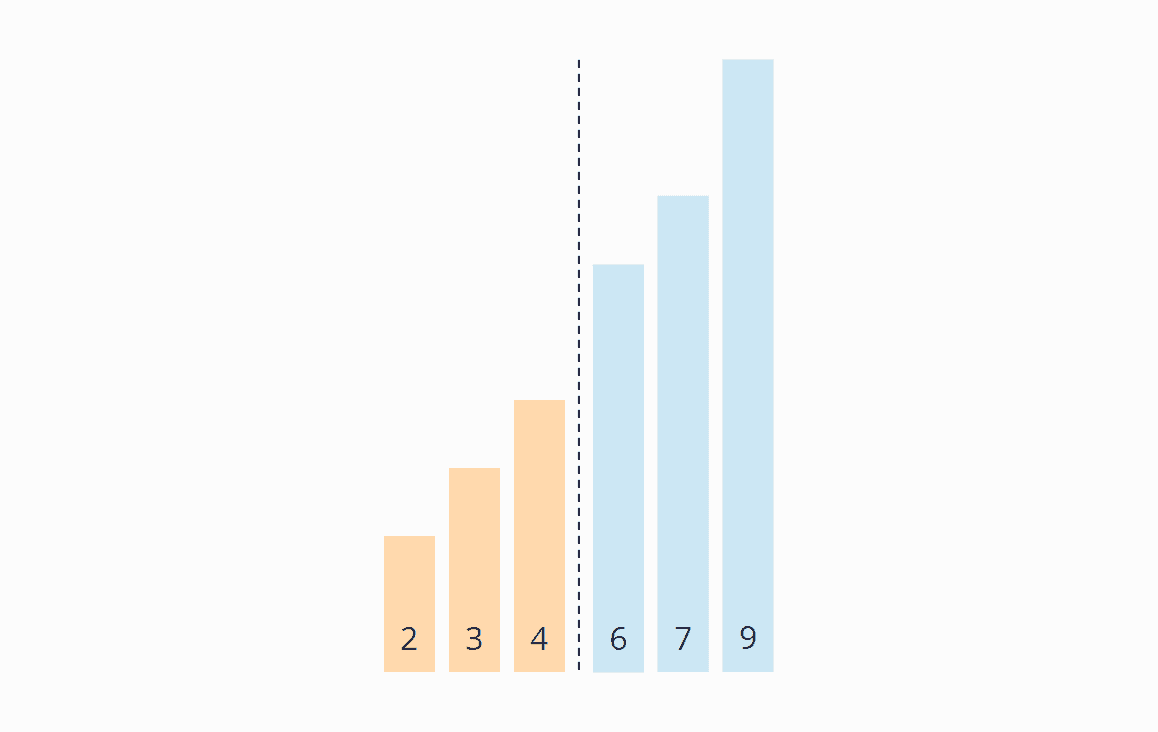
Iteration 4
Wir beginnen wieder am Anfang des Arrays. Im unsortierten Bereich müssen weder die 2 und 3 noch die 3 und 4 vertauscht werden. Damit sind alle Elemente sortiert und wir können den Algorithmus beenden.
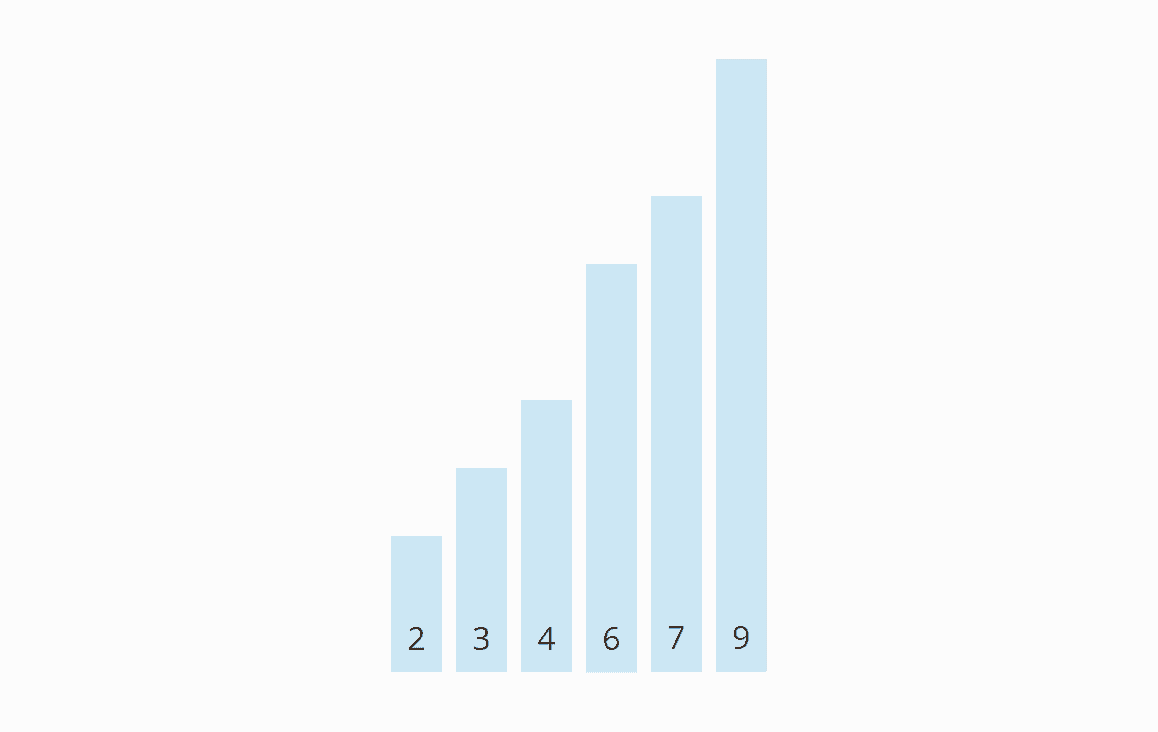
Herkunft des Namens
Wenn wir die Vertauschoperationen des vorherigen Beispiels animieren, steigen die Elemente nach und nach bis zu ihren Zielpositionen auf – ähnlich wie Luftblasen (english: "bubbles"), daher der Name "Bubble Sort":
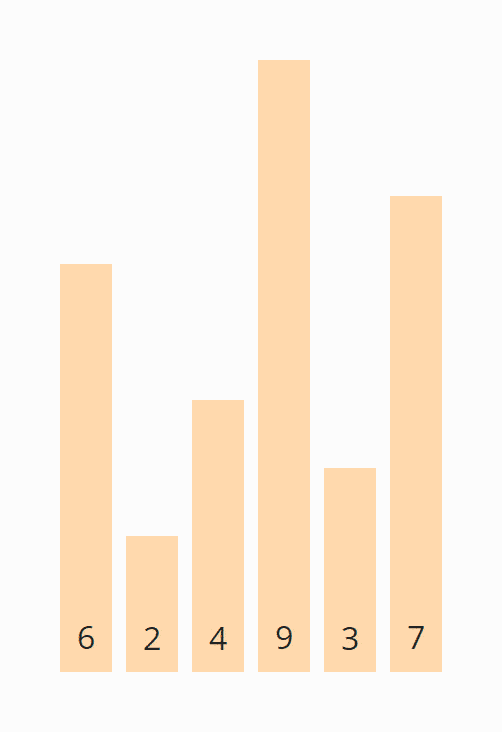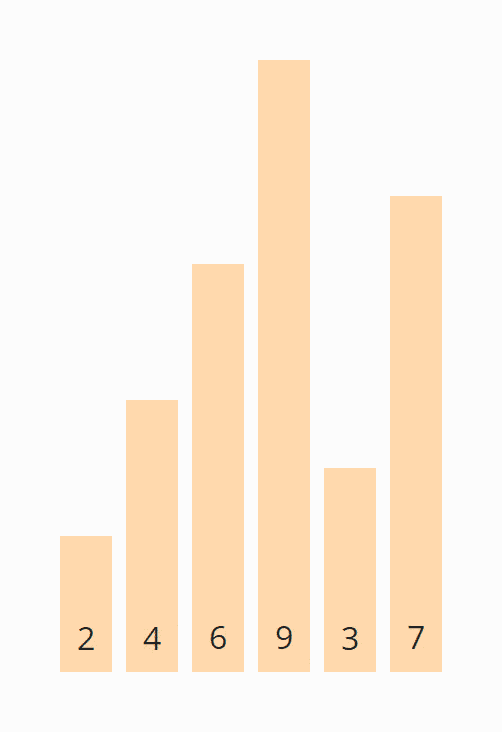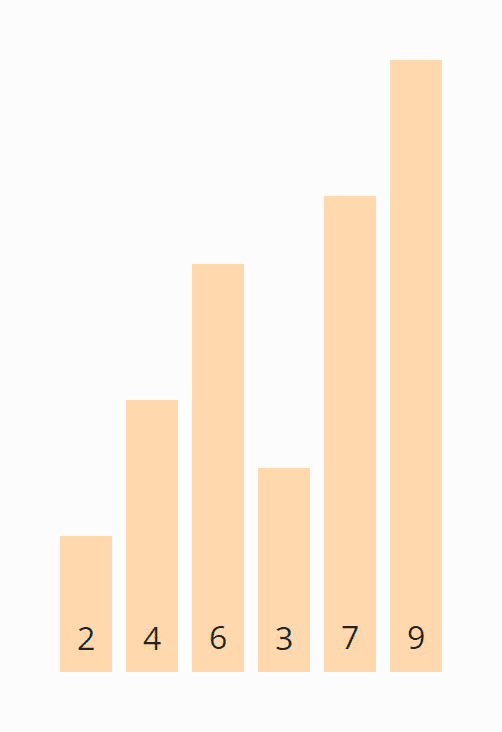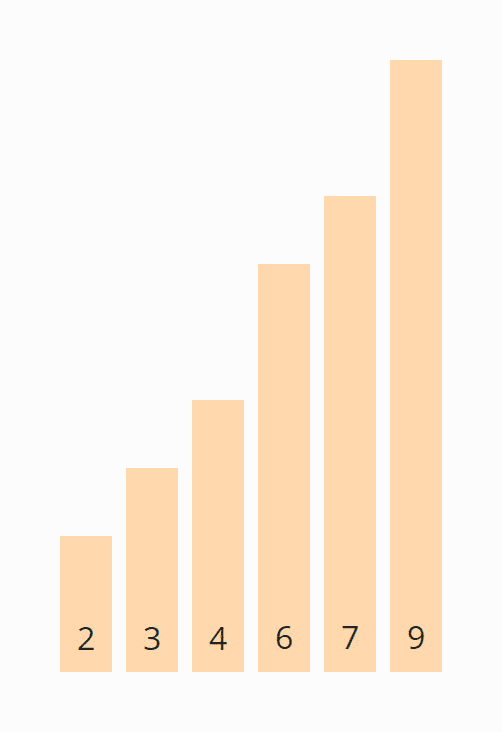
Bubble Sort Java Quellcode
Im folgenden findest Du die oben beschriebene, optimierte Implementierung von Bubble Sort.
Da in der ersten Iteration das größte Element bis ganz nach rechts wandert, in der zweiten Iteration das zweitgößte bis zur zweitletzten Position, usw., müssen wir in jeder Iteration ein Element weniger vergleichen als in der vorherigen.
(Im Beispiel im vorangegangenen Abschnitt hatte ich das durch die Bereichsgrenze dargestellt, die nach jeder Iteration um eine Position nach links wandert.)
Dazu dekrementieren wir in der äußeren Schleife den Wert max, beginnend bei elements.length - 1, in jeder Iteration um eins.
Die innere Schleife vergleicht dann jeweils zwei Elemente bis zur Position max miteinander und vertauscht diese, wenn das linke Element größer ist als das rechte.
Wurden in einer Iteration keine Elemente vertauscht (d. h. swapped ist false), endet der Algorithmus vorzeitig.
public class BubbleSortOpt1 {
public static void sort(int[] elements) {
for (int max = elements.length - 1; max > 0; max--) {
boolean swapped = false;
for (int i = 0; i < max; i++) {
int left = elements[i];
int right = elements[i + 1];
if (left > right) {
elements[i + 1] = left;
elements[i] = right;
swapped = true;
}
}
if (!swapped) break;
}
}
}Code-Sprache: Java (java)Der abgebildete Code unterscheidet sich leicht von der Klasse BubbleSortOpt1 im GitHub-Repository: Diese implementiert das Interface SortAlgorithm, um innerhalb des Testframeworks austauschbar zu sein.
Die nicht-optimierte Variante – in der der Algorithmus in jeder Iteration alle Elemente bis zum Ende vergleicht – findest du in der Klasse BubbleSort.
In der Klasse BubbleSortOpt2 findest du einen theoretisch noch stärker optimierten Algorithmus. Es kann nämlich auch sein, dass nach der n-ten Iteration, nicht nur die letzten n Elemente sortiert sind, sondern mehr – je nachdem, wie die Elemente ursprünglich angeordnet waren.
Diese Variante zählt daher max nicht um jeweils 1 herunter, sondern setzt max nach jeder Iteration auf die Position desjenigen Elements, das zuletzt vertauscht wurde. Der Test CompareBubbleSorts zeigt allerdings, dass diese Variante in der Praxis langsamer ist:
----- Results after 50 iterations-----
BubbleSort -> fastest: 772.6 ms, median: 790.3 ms
BubbleSortOpt1 -> fastest: 443.2 ms, median: 452.7 ms
BubbleSortOpt2 -> fastest: 497.0 ms, median: 510.0 ms Code-Sprache: Klartext (plaintext)Die vollständige Ausgabe des Testprogramms findest Du in der Datei TestResults_BubbleSort_Algorithms.log.
Warum ist die zweite optimierte Variante langsamer? Meine Vermutung ist, dass das Speichern und das (innerhalb einer Iteration) mehrfache Aktualisieren der Position des zuletzt vertauschten Elements deutlich teurer ist als das (pro Iteration) maximal einmalige Ändern des swapped-Werts.
Bubble Sort Zeitkomplexität
Wir bezeichnen die Anzahl der zu sortierenden Elemente mit n, im Beispiel oben wäre n = 6.
Die zwei ineinander verschachtelten Schleifen lassen vermuten, dass wir es bei Bubble Sort mit quadratischem Aufwand zu tun haben, also einer Zeitkomplexität* von O(n²). Dies wäre dann der Fall, wenn beide Schleifen bis zu einem Wert iteratieren, der linear mit n steigt.
Dies ist bei Bubble Sort nicht ganz so einfach nachzuweisen, wie z. B. bei Insertion Sort oder Selection Sort.
Bei Bubble Sort müssen wir best, worse und average case separat betrachten. Dies geschieht in den folgenden Unterabschnitten.
* Die Begriffe „Zeitkomplexität“ und „O-Notation“ (ausgesprochen „Groß O-Notation“) erkläre ich in diesem Artikel anhand von Beispielen und Diagrammen.
Zeitkomplexität im best case
Fangen wir mit dem einfachsten Fall an: Falls die Zahlen bereits aufsteigend sortiert sind, wird der Algorithmus in der ersten Iteration feststellen, dass keine Zahlenpaare vertauscht werden müssen und daraufhin umgehend terminieren.
Dabei muss der Algorithmus n-1 Vergleiche durchführen; also gilt:
Die Zeitkomplexität von Bubble Sort beträgt im best case: O(n)
Zeitkomplexität im worst case
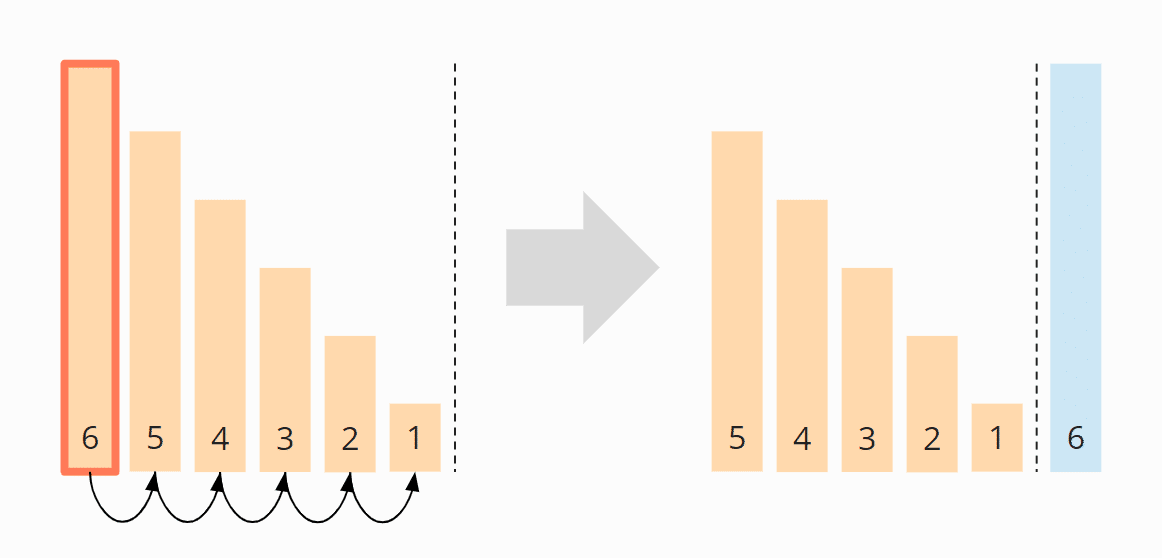
Den worst case demonstriere ich an einem Beispiel. Nehmen wir an, wir wollen das absteigend sortierte Array [6, 5, 4, 3, 2, 1] mit Bubble Sort sortieren.
In der ersten Iteration wandert das größte Element, die 6, von ganz links nach ganz rechts. Die fünf Einzelschritte (Vertauschen der Paare 6/5, 6/4, 6/3, 6/2, 6/1) habe ich in der Abbildung weggelassen:
In der zweiten Iteration wird das zweitgrößte Element, die 5, von ganz links – über vier Zwischenschritte – an die vorletzte Position verschoben:

In der dritten Iteration wird die 4 – über drei Zwischenschritte – an die drittletzte Stelle geschoben:

In der vierten Iteration wird die 3 – über zwei Einzelschritte – an ihre finale Position verschoben:

Und zuletzt werden die 2 und die 1 vertauscht:

In Summe haben wir also 5 + 4 + 3 + 2 + 1 = 15 Vergleichs- und Tauschoperationen.
Das können wir auch wie folgt ausrechnen:
Sechs Elemente mal fünf Vergleichs- und Tauschoperationen; geteilt durch zwei, da im Mittel über alle Iterationen die Hälfte der Elemente verglichen und verschoben wird:
6 × 5 × ½ = 30 × ½ = 15
Ersetzen wir 6 durch n, erhalten wir:
n × (n – 1) × ½
Ausmultipliziert ergibt das:
½ (n² – n)
Die höchste Potenz von n in diesem Term ist n²; es gilt also:
Die Zeitkomplexität von Bubble Sort beträgt im worst case: O(n²)
Zeitkomplexität im average case
Die durchschnittliche Zeitkomplexität lässt sich bei Bubble Sort – im Gegensatz zu den meisten anderen Sortieralgorithmen – leider nicht auf anschauliche Art und Weise erklären.
Ohne dies mathematisch zu beweisen (das würde den Rahmen dieses Artikels sprengen) kann man grob sagen, dass man im average case etwa halb so viele Tauschoperationen hat wie im worst case, da sich etwa die Hälfte der Elemente im Vergleich zum Nachbarelement an der richtigen Position befindet. Die Anzahl der Tauschoperationen ist also:
¼ (n² – n)
Bei der Anzahl der Vergleichsoperationen wird es noch komplizierter, diese beträgt (Quelle: Wikipedia):
½ (n² - n × ln(n) - (? + ln(2) - 1) × n) + O(√n)
In beiden Termen ist die höchste Potenz von n wieder n², so dass gilt:
Die Zeitkomplexität von Bubble Sort beträgt im average case: O(n²)
Laufzeit des Java Bubble Sort-Beispiels
Überprüfen wir die Theorie mit einem Test! Im GitHub-Repository findest du das Programm UltimateTest, das Bubble Sort (und alle anderen in dieser Artikelserie vorgestellten Sortieralgorithmen) nach folgenden Kriterien testet:
- für Array-Größen beginnend ab 1.024 Elementen, mit einer Verdoppelung nach jeder Iteration, bis entweder eine Array-Größe von 536.870.912 erreicht ist (= 229) oder ein Sortiervorgang länger als 20 Sekunden dauert;
- für unsortierte, aufsteigend und absteigend vorsortierte Elemente;
- mit zwei Warm-Up-Runden, um dem HotSpot-Compiler ausreichend Zeit zu geben, um den Code zu optimieren.
Das ganze wird so oft wiederholt, bis der Prozess abgebrochen wird. Nach jeder Wiederholung gibt das Program den Median aller bisherigen Messergebnisse aus.
Hier das Ergebnis für Bubble Sort nach 50 Iterationen:
| n | unsortiert | absteigend | aufsteigend |
|---|---|---|---|
| ... | ... | ... | ... |
| 8.192 | 61,73 ms | 35,18 ms | 0,004 ms |
| 16.384 | 294,64 ms | 141,16 ms | 0,008 ms |
| 32.768 | 1.272,07 ms | 566,39 ms | 0,015 ms |
| 65.536 | 5.196,82 ms | 2.267,85 ms | 0,030 ms |
| 131.072 | 20.903,54 ms | 9.068,25 ms | 0,060 ms |
| 262.144 | – | – | 0,129 ms |
| ... | ... | ... | ... |
| 536.870.912 | – | – | 192,509 ms |
Dies ist nur ein Auszug, das vollständige Ergebnis findest Du hier.
Hier die Ergebnisse noch einmal als Diagramm:
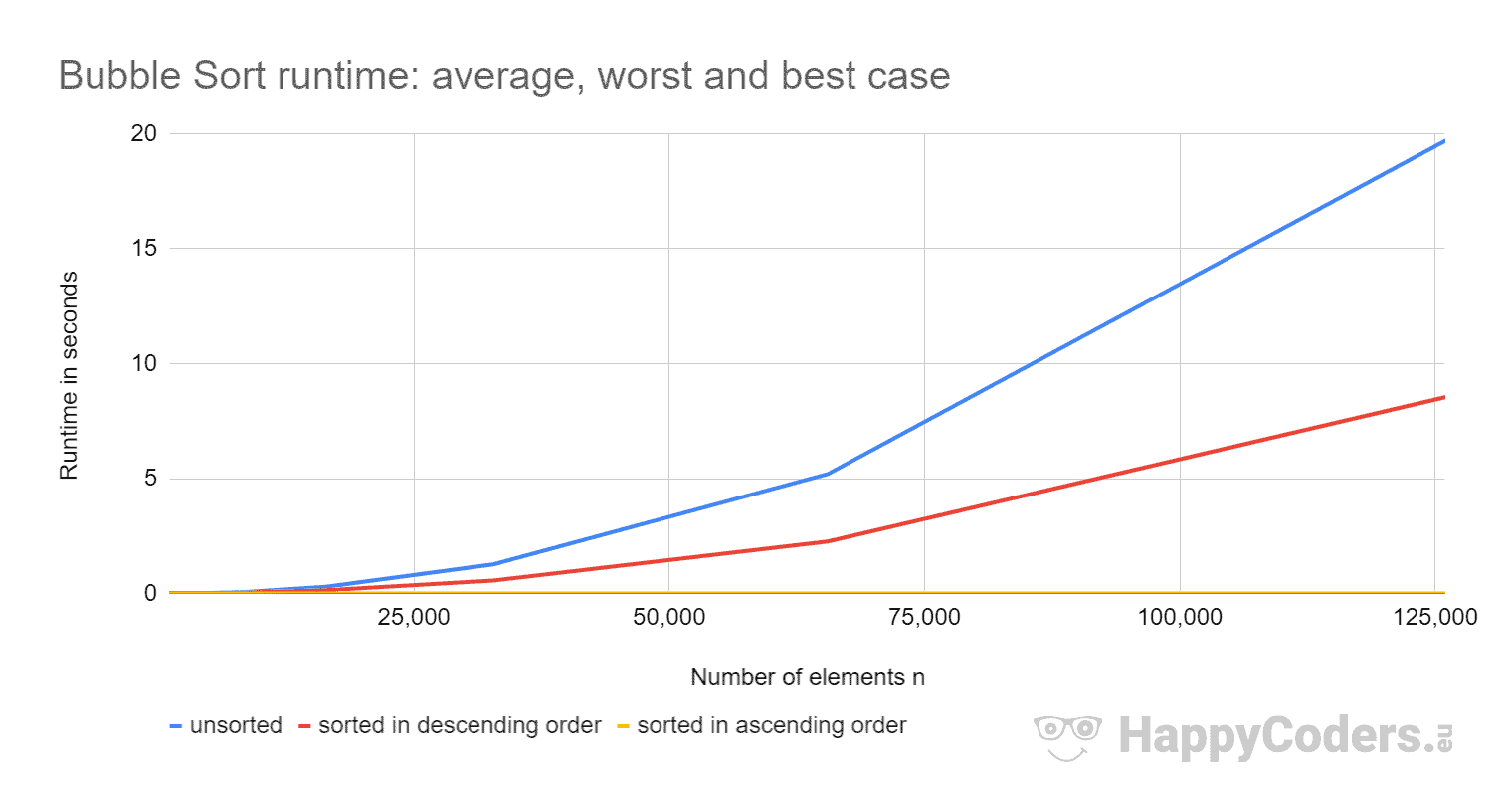
Bei aufsteigend vorsortierten Elementen ist Bubble Sort so schnell, dass die Kurve keinen Ausschlag nach oben zeigt. Deshalb ist hier die Kurve noch einmal einzeln:
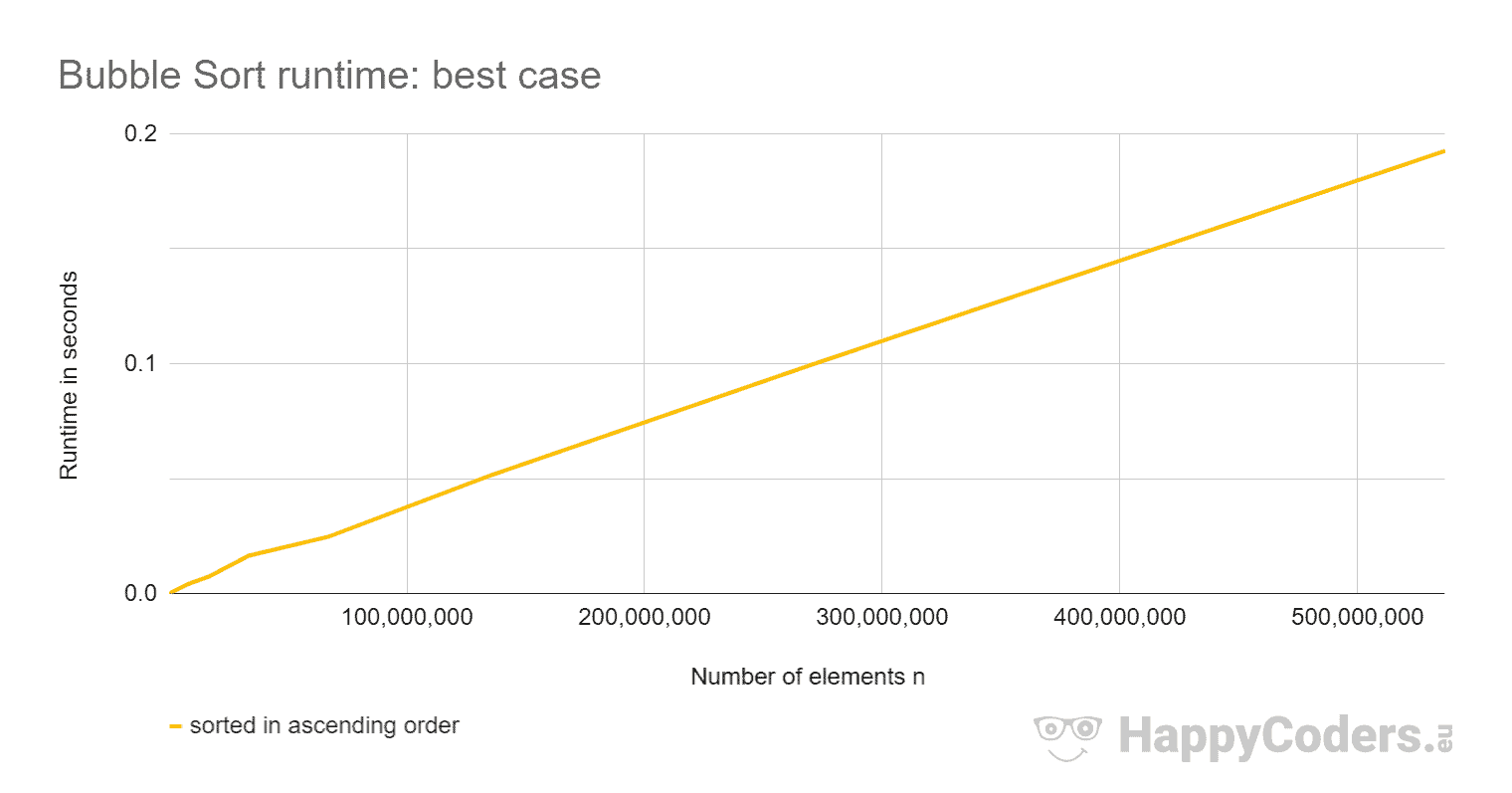
Es lässt sich sehr gut erkennen, ...
- dass sich die Laufzeit bei Verdopplung der Eingabemenge bei unsortierten und absteigend sortierten Elementen in etwa vervierfacht;
- dass die Laufzeit bei aufsteigend sortierten Elementen linear wächst und um Größenordnungen kleiner ist als bei unsortierten Elementen;
- dass die Laufzeit im average case etwas mehr als doppelt so hoch ist wie im worst case.
Die ersten zwei Beobachtungen entsprechen den Erwartungen.
Doch warum ist die Laufzeit im average case so viel höher als im worst case? Müssten wir dort nicht nur etwa halb so viele Tauschoperationen haben und zumindest minimal weniger Vergleiche – und dementsprechend eher die halbe Zeit als die doppelte?
Tausch- und Vergleichsoperationen im average und worst case
Um das zu prüfen, nutze ich das Programm CountOperations, um die Anzahl der verschiedenen Operationen anzeigen zu lassen. Hier sind die Ergebnisse für unsortierte und absteigend sortierte Elemente in einer Tabelle zusammengefasst:
| n | Tauschen unsortiert | Tauschen absteigend | Vergleiche unsortiert | Vergleiche absteigend |
|---|---|---|---|---|
| ... | ... | ... | ... | ... |
| 128 | 8.050 | 16.256 | 8.136 | 8.255 |
| 256 | 31.854 | 65.280 | 32.893 | 32.895 |
| 512 | 128.340 | 261.632 | 130.767 | 131.327 |
| 1.024 | 528.004 | 1.047.552 | 524.475 | 524.799 |
| 2.048 | 2.111.760 | 4.192.256 | 2.097.546 | 2.098.175 |
| ... | ... | ... | ... | ... |
Die Ergebnisse bestätigen die Annahme: Bei unsortierten Elementen haben wir etwa halb so viele Tauschoperationen und minimal weniger Vergleiche als bei absteigend sortierten Elementen.
Warum ist Bubble Sort für absteigend sortierte Elemente schneller als für zufällig verteilte Elemente?
Wie kann es sein, dass Bubble Sort bei absteigend sortierten Element trotz doppelt so vieler Tauschoperationen so viel schneller ist als bei zufällig angeordneten Elementen?
Die Ursache für diese Diskrepanz ist in der Sprungvorhersage (englisch "branch prediction") zu finden:
Wenn die Elemente absteigend sortiert sind, dann ist das Resultat der Vergleichsoperation if (left > right) im unsortierten Bereich immer true und im sortierten Bereich immer false.
Wenn die Sprungvorhersage davon ausgeht, dass das Ergebnis eines Vergleichs immer dasselbe ist wie das des vorangegangenen Vergleichs, dann hat sie mit dieser Annahme – mit einer einzigen Ausnahme: an der Bereichsgrenze – immer Recht. Somit kann die Befehls-Pipeline der CPU die meiste Zeit voll ausgenutzt werden.
Bei unsortierten Daten hingegen können keine verlässlichen Vorhersagen über das Ergebnis des Vergleichs getroffen werden, so dass die Pipeline häufig gelöscht und neu gefüllt werden muss.
Weitere Eigenschaften von Bubble Sort
In diesem Abschnitt geht es um die Platzkomplexität, Stabilität und Parallelisierbarkeit von Bubble Sort.
Platzkomplexität von Bubble Sort
Bubble Sort benötigt neben der Schleifenvariablen max und den Hilfsvariablen swapped, left und right keinen zusätzlichen Speicherplatz.
Die Platzkomplexität von Bubble Sort ist somit O(1).
Stabilität von Bubble Sort
Dadurch, dass immer zwei nebeneinander liegende Elemente miteinander verglichen werden – und diese nur dann vertauscht werden, wenn das linke Element größer ist als das rechte, können Elemente mit gleichem Key niemals die Position relativ zueinander tauschen.
Dazu müssten, wie beispielsweise bei Selection Sort, zwei Elemente über mehr als eine Position hinweg ihre Plätze tauschen. Das kann hier nicht passieren.
Bubble Sort ist somit ein stabiler Sortieralgorithmus.
Parallelisierbarkeit von Bubble Sort
Es gibt zwei Ansätze, um Bubble Sort zu parallelisieren:
Ansatz 1 "Odd-even sort"
Man vergleicht parallel das erste mit dem zweiten Element, das dritte mit dem vierten, das fünfte mit dem sechsten, usw. und vertauscht die jeweiligen Elemente, wenn das linke größer ist als das rechte.
Danach vergleicht man das zweite Element mit dem dritten, das vierte mit dem fünften, das sechste mit dem siebten usw.
Diese zwei Schritte führt man abwechselnd durch, solange bis in beiden Schritten keine Elemente mehr vertauscht werden:

Diesen Algorithmus bezeichnet man auch als "Odd–even sort".
Du findest den Quellcode in der Klasse BubbleSortParallelOddEven im GitHub-Repository.
Die Synchronisation zwischen den Schritten (die Threads dürfen mit einem Schritt erst dann beginnen, wenn alle Threads den vorherigen Schritt beendet haben), erfolgt dabei mit einem Phaser.
Ansatz 2 "Divide and Conquer"
Man teilt das zu sortierende Array in so viele Bereiche ("Partitionen"), wie man Cores zur Verfügung hat.
Nun führt man eine Bubble-Sort-Iteration in allen Partitionen parallel durch. Man wartet, bis alle Threads fertig sind, und vergleicht dann jeweils das letzte Element einer Partition mit dem ersten der nächsten Partition. Wenn auch damit alle Threads fertig sind, beginnt der Vorgang von vorne.
Diese Schritte wiederholt man solange, bis in allen Threads keine Elemente mehr vertauscht werden:

Du findest den Quellcodes des Algorithmus in der Klasse BubbleSortParallelDivideAndConquer im GitHub-Repository.
Auch hier wird zur Synchronisation der Threads ein Phaser verwendet. Tatsächlich ist ein Großteil des Codes beider Algorithmen gleich, da auch für den Odd-Even-Ansatz das Array in Partitionen aufgeteilt wird. Den gemeinsamen Code habe ich in die abstrakte Basisklasse BubbleSortParallelSort verschoben.
Bubble Sort parallel: Performance
Die Performance der parallelen Varianten vergleiche ich mit dem oben bereits genannten Test CompareBubbleSorts. Hier das Ergebnis für die parallelen Algorithmen, verglichen mit der schnellsten sequentiellen Variante:
----- Results after 50 iterations-----
BubbleSortOpt1 -> fastest: 443.2 ms, median: 452.7 ms
BubbleSortParallelOddEven -> fastest: 62.6 ms, median: 68.6 ms
BubbleSortParallelDivideAndConquer -> fastest: 126.8 ms, median: 145.7 ms Code-Sprache: Klartext (plaintext)Die "odd-even"-Variante ist auf meiner 6-Core-CPU (12 virtuelle Kerne mit Hyper-Threading) und bei 20.000 unsortierten Elementen also 6,6 mal schneller als die sequentielle Variante.
Der "divide-and-conquer"-Ansatz ist nur 3,1 mal schneller. Dies dürfte daran liegen, dass jeder Thread im zweiten Teilschritt der Iteration jeweils nur einen Vergleich durchführt. Demgegenüber steht ein relativ hoher Synchronisationsaufwand durch den Phaser.
Zusammenfassung
Bubble Sort ist ein einfach zu implementierender, stabiler Sortieralgorithmus mit einer Zeitkomplexität von O(n²) im average und worst case – und O(n) im best case.
Weitere Sortieralgorithmen findest du in dieser Übersicht aller Sortieralgorithmen und ihrer Eigenschaften im ersten Teil der Artikelserie.
Bubble Sort war das letzte einfache Sortierverfahren dieser Artikelserie; im nächsten Teil steigen wir mit Quicksort in die effizienten Sortierverfahren ein.
