

Wie findet ein Navigationssystem den schnellsten Weg vom Start zum Ziel in möglichst geringer Zeit? Dieser Frage (und ähnlichen) geht diese Artikelserie über "Shortest Path"-Algorithmen nach.
Im vorangegangenen Teil über Dijkstras Algorithmus haben wir festgestellt, dass dieser vom Startpunkt aus erreichbaren Pfaden in alle Richtungen folgt – und zwar unabhängig davon, in welcher Richtung sich das Ziel befindet. Das ist natürlich nicht optimal.
Der A*-Algorithmus (ausgesprochen "A Stern" oder englisch "A Star") ist eine Weiterentwicklung des Dijkstra-Algorithmus. Der A*-Algorithmus beendet die Prüfung von Pfaden, die in die falsche Richtung führen, vorzeitig. Dazu verwendet er eine Heuristik, die mit minimalem Aufwand für jeden Knoten die kürzestmögliche Entfernung zum Ziel berechnen kann. Wie das genau funktioniert, erfährst du in diesem Artikel.
Die Themen im Einzelnen:
- Wie funktioniert der A*-Algorithmus (Schritt für Schritt an einem Beispiel erklärt)
- Was unterscheidet den A*-Algorithmus von Dijkstras Algorithmus?
- Wie implementiert man den A*-Algorithmus in Java?
- Wie bestimmt man die Zeitkomplexität?
- Messung der Laufzeit der Java-Implementierung
Den Quellcode zur gesamten Artikelserie findest du in meinem GitHub-Repository.
A*-Algorithmus – Beispiel
Wir beginnen mit einem Beispiel. Der Einfachheit halber verwenden wir das gleiche Beispiel wie bei der Erklärung des Dijkstra-Algorithmus. Die folgende Zeichnung stellt eine Straßenkarte dar:

Orte werden durch Kreise mit Buchstaben dargestellt. Die Linien dazwischen sind Schnellstraßen (dicke Linien), Dorfstraßen (dünne Linien) und Feldwege (gestrichelte Linien).
Die Straßenkarte bilden wir auf den folgenden Graphen ab. Orte werden zu Knoten; Straße und Wege werden zu Kanten:

Die Gewichte der Kanten stellen die Kosten eines Weg dar. Das ist beispielsweise die Zeit in Minuten, die man für das Zurücklegen eines Weges benötigt.
Ein kürzerer Weg führt nicht zwingendermaßen zu niedrigeren Kosten. Es kann z. B. deutlich länger dauern einen kurzen Feldweg zu passieren als eine lange Schnellstraße.
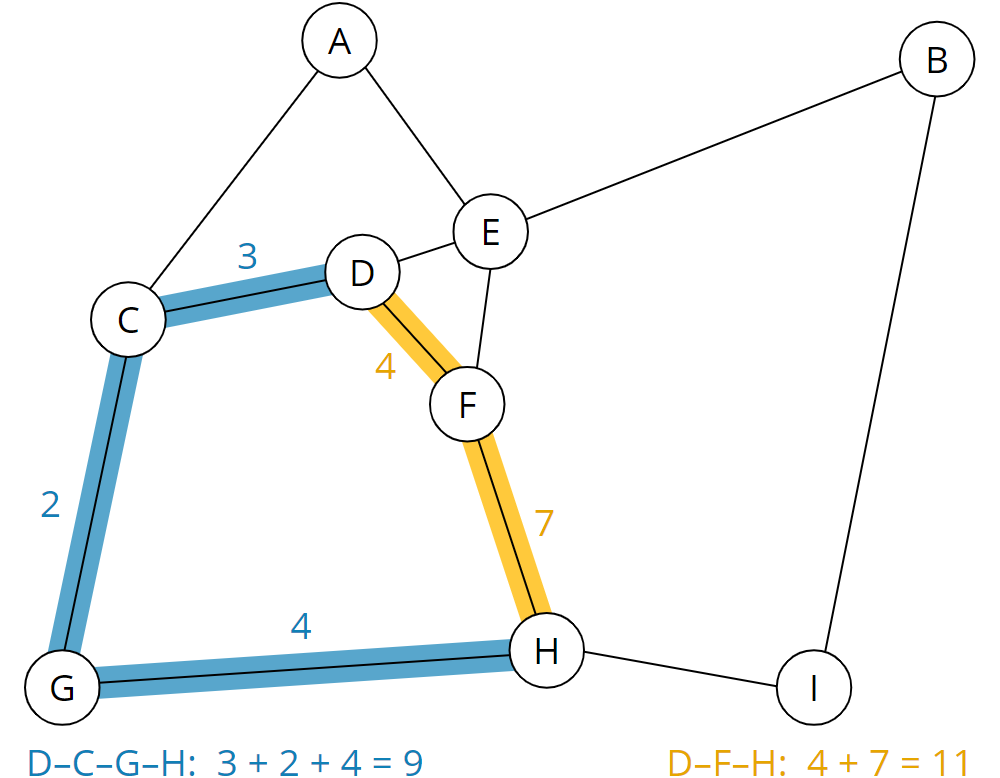
Wir können nun z. B. ablesen, dass der kürzeste Weg von D nach H über F führt und insgesamt 11 Minuten dauert (gelbe Strecke). Über die längere Strecke über C und G (blaue Strecke) brauchen wir hingegen nur 9 Minuten:
Wir Menschen schaffen das mit einem Blick. Auch auf komplexeren Straßenkarten können wir relativ problemlos navigieren. Die erfahreneren von uns können sich sicher noch gut an die Zeiten erinnern, zu denen wir im Auto auf eine Straßenkarte blickten anstatt auf ein Navigationssystem.
Ein Computer braucht hierfür einen Algorithmus, z. B. den A*-Algorithmus.
A*-Algorithmus – Heuristik-Funktion
In der Einleitung habe ich eine Heuristik-Funktion erwähnt, die den schnellstmöglichen Weg von allen Knoten des Graphen zum Zielknoten berechnen kann. Da unser Graph eine zweidimensionale Landkarte repräsentiert, eignet sich für die Heuristik-Funktion die euklidische Distanz oder – lapidar gesagt – die Luftlinie zum Ziel-Knoten.
Die Heuristik wird im späteren Verlauf dafür sorgen, dass der Algorithmus bei der Wegsuche diejenigen Knoten priorisiert, die grob in die richtige Richtung führen.
Wichtig ist dabei, dass die Heuristik die tatsächlichen Kosten, die bis zum Ziel anfallen könnten, niemals überschätzen darf. Damit wir im Beispiel die tatsächlichen Kosten zum Ziel nicht überschätzen, berechnen wir als Heuristik die Anzahl der Minuten, die man auf einer der Luftlinie folgenden Schnellstraße zum Ziel benötigen würde.
Um Entfernungen messen zu können, fügen wir ein Koordinatensystem hinzu:

Wir berechnen nun die Länge der zwei Schnellstraßen von A nach C und von C nach G mit Hilfe des Satzes des Pythagoras. Dann teilen wir die Länge durch die Kosten der Strecke, um die Geschwindigkeit zu erhalten:
| Weg A–C | Entfernung: 3,414 km Kosten: 2 min Geschwindigkeit: 3,414 km / 2 min = 1,707 km/min (= 102,42 km/h) |
| Weg C–G | Entfernung: 3,406 km Kosten: 2 min Geschwindigkeit: 3,406 km / 2 min = 1,703 km/min (= 102,18 km/h) |
Die schnellstmögliche Geschwindigkeit (vmax) auf unserer Karte wird also auf der Strecke A–C erreicht und beträgt etwa 1,7 km/min (dies entspricht 102 km/h).
Eigentlich müssten wir die Geschwindigkeit für alle Wege berechnen. Aber wir hatten die Karte ja initial so konstruiert, dass alle anderen Straßen langsamer sind. Deshalb sparen wir uns das an dieser Stelle.
In einem Navigationssystem ist die schnellstmögliche Geschwindigkeit vorberechnet und in den Kartendaten enthalten.
Anwendung der Heuristik-Funktion
Mit Hilfe der schnellstmöglichen Geschwindigkeit vmax berechnen wir nun die kürzest mögliche Fahrtzeit von jedem Punkt der Karte zum Zielpunkt. Dazu berechnen wir jeweils die Entfernung in Form der euklidische Distanz und teilen diese durch vmax.
Für Knoten A beispielsweise wie folgt:
| Knoten A | Entfernung zu Zielknoten H: 6,588 km vmax: 1,707 km/min Minimale Kosten: 6,588 km / 1,707 km/min = 3,859 min ≈ 3,9 min |
Genauso gehen wir für alle anderen Knoten vor. Es ergeben sich folgende kürzestmögliche Fahrtzeiten (auf eine Nachkommastelle gerundet):

Vorbereitung – Tabelle der Knoten
Zur weiteren Vorbereitung erstellen wir eine Tabelle der Knoten. Die Tabelle hat folgende Spalten:
- Knotenname
- Vorgänger-Knoten
- Gesamtkosten vom Start-Knoten
- Minimale Restkosten zum Ziel-Knoten
- Summe beider Kosten
Die Vorgänger-Knoten bleiben zunächst leer. Als Gesamtkosten vom Start tragen wir für den Startknoten selbst eine 0 ein; für alle anderen Knoten unendlich, da wir noch nicht wissen, ob diese vom Startknoten überhaupt erreichbar sind.
Als minimale Restkosten tragen wir die im vorherigen Abschnitt berechneten Restkosten zum Zielknoten ein.
Die Tabelle wird letztlich nach der Summe der zwei Kostenspalten (Gesamtkosten vom Start-Knoten + Minimale Restkosten zum Ziel-Knoten) sortiert. Die Knoten, bei der die Summe der Kosten unendlich ist, bleiben unsortiert (im Beispiel sind sie alphabetisch sortiert):
| Knoten | Vorgänger | Gesamtkosten vom Start | Minimale Restkosten zum Ziel | Summe aller Kosten |
|---|---|---|---|---|
| D | – | 0,0 | 2,5 | 2,5 |
| A | – | ∞ | 3,9 | ∞ |
| B | – | ∞ | 4,3 | ∞ |
| C | – | ∞ | 3,2 | ∞ |
| E | – | ∞ | 2,5 | ∞ |
| F | – | ∞ | 1,5 | ∞ |
| G | – | ∞ | 2,8 | ∞ |
| H | – | ∞ | 0,0 | ∞ |
| I | – | ∞ | 1,6 | ∞ |
Im folgenden ist es wichtig die Begriffe Kosten, Gesamtkosten und Restkosten zu unterscheiden:
- Kosten bezeichnet die Kosten von einem Knoten zu seinen Nachbarknoten.
- Gesamtkosten bezeichnet die Summe aller Teilkosten vom Startknoten über eventuelle Zwischenknoten zu einem bestimmten Knoten.
- Restkosten bezeichnet die durch die Heuristik-Funktion berechneten Kosten, die auf dem Weg zum Ziel noch mindestens entstehen werden.
A*-Algorithmus Schritt für Schritt – Abarbeitung der Knoten
In den folgenden Grafiken stelle ich in den Knoten den jeweiligen Vorgängerknoten sowie die Gesamt- und Restkosten mit dar. Diese Daten sind in der Regel nicht im Graph enthalten, sondern nur in der oben beschriebenen Tabelle. Sie hier mit anzuzeigen wird das Verständnis erleichtern.
Schritt 1: Betrachten aller Nachbarn des Startpunkts
Wir entnehmen das erste Element – Knoten D – aus der Tabelle und betrachten seine Nachbarn, also C, E und F:

Die Gesamtkosten der Nachbarknoten stehen zu diesem Zeitpunkt noch auf dem Initialwert unendlich, was bedeutet, dass wir bisher noch keine Wege dorthin gefunden haben. Nun haben wir Wege dorthin gefunden – nämlich direkt vom Ausgangspunkt D.
Wir tragen daher als Gesamtkosten vom Start die Kosten von D zum jeweiligen Knoten ein und bilden die Summe mit den Restkosten. Außerdem hinterlegen wir Knoten D als Vorgänger.
Für C beispielsweise ergeben sich folgende Werte:
- Gesamtkosten vom Start: 3,0 (die Kosten von D zu C)
- Restkosten: 3,2 (diese haben wir im vorherigen Abschnitt für alle Knoten berechnet)
- Summe aller Kosten: 3,0 + 3,2 = 6,2
Für E und F gehen wir genauso vor. Für ein einfaches Verständnis trage ich die Ergebnisse in den Graph ein:

Die aktualisierte Tabelle sortieren wir erneut nach der Summe der Kosten (die geänderten Einträge sind fett markiert):
| Knoten | Vorgänger | Gesamtkosten vom Start | Minimale Restkosten zum Ziel | Summe aller Kosten |
|---|---|---|---|---|
| E | D | 1,0 | 2,5 | 3,5 |
| F | D | 4,0 | 1,5 | 5,5 |
| C | D | 3,0 | 3,2 | 6,2 |
| A | – | ∞ | 3,5 | ∞ |
| B | – | ∞ | 3,8 | ∞ |
| G | – | ∞ | 2,8 | ∞ |
| H | – | ∞ | 0,0 | ∞ |
| I | – | ∞ | 1,6 | ∞ |
Die Änderungen sind so lesen: Knoten E, F und C wurden entdeckt. Sie können über D in 1, 4 bzw. 3 Minuten erreicht werden. Addiert man die minimalen Restkosten zum Ziel, ergeben sich 3,5, 5,5 und 6,2 Minuten, die man über die jeweiligen Knoten mindestens brauchen würde, um das Ziel zu erreichen.
Unterschied zum Dijkstra-Algorithmus: Umwege werden gemieden
Hier wird bereits der Unterschied zum Dijkstra-Algorithmus deutlich. Dort hatten wir die Tabelle nach Gesamtkosten sortiert, weshalb Knoten C (Gesamtkosten 3,0) vor Knoten F (Gesamtkosten 4,0) einsortiert wurde.
Durch die heuristische Komponente liegt beim A*-Algorithmus Knoten F (Kostensumme 5,3) vor Knoten C (Kostensumme 5,8). Der A*-Algorithmus hält es also für wahrscheinlicher das Ziel schneller über Knoten F zu erreichen als über Knoten C. Wenn wir noch einmal einen Blick auf denjenigen Ausschnitt der Karte werden, den der Algorithmus bis jetzt betrachtet hat, macht das Sinn:

Knoten F liegt in der direkten Richtung zum Zielknoten H, während der Weg über Knoten C in die falsche Richtung führt.
Dass der Umweg über Knoten C letztendlich schneller ist, wird A* bald feststellen. In der Regel sind Umwege aber länger. Deshalb ist es gerechtfertig, diese niedriger zu priorisieren.
Schritt 2: Betrachten aller Nachbarn von Knoten E
Wir wiederholen den Prozess für denjenigen Knoten, der jetzt an erster Stelle der Tabelle steht. Das ist Knoten E. Wir entnehmen ihn und betrachten seine Nachbarn, A, B, D und F:

Knoten D ist in der Tabelle nicht mehr enthalten. Dies bedeutet, dass wir den kürzesten Weg dorthin bereits entdeckt haben (es ist der Startknoten, den wir im vorangegangenen Schritt behandelt haben). Wir können ihn daher an dieser Stelle ignorieren.
Knoten A und B haben als Gesamtkosten unendlich, d. h. zu ihnen wurde noch kein Weg gefunden. Wir berechnen für diese Knoten die Gesamtkosten vom Start, in dem wir die Gesamtkosten des aktuellen Knotens E und die Kosten von Knoten E zu Knoten A bzw. B addieren:
| Knoten A | 1,0 (Gesamtkosten vom Start zu E) + 3,0 (Kosten E–A) = 4,0 |
| Knoten B | 1,0 (Gesamtkosten vom Start zu E) + 5,0 (Kosten E–B) = 6,0 |
Zu den jeweiligen Gesamtkosten addieren wir die vorab berechneten minimalen Restkosten zum Ziel:
| Knoten A | 4,0 (Gesamtkosten vom Start zu A) + 3,9 (minimale Restkosten von A zum Ziel) = 7,9 |
| Knoten B | 6,0 (Gesamtkosten vom Start zu B) + 4,3 (minimale Restkosten von B zum Ziel) = 10,3 |
Wir aktualisieren die Einträge in der Grafik:

Zu Knoten F wurde bereits ein Weg gefunden mit Gesamtkosten von 4. Es wäre möglich, dass der Weg über den aktuellen Knoten E schneller ist. Um dies zu prüfen, berechnen wir auch für Knoten F die Gesamtkosten über E:
| Knoten F | 1,0 (Gesamtkosten vom Start zu E) + 6,0 (Kosten E–F) = 7,0 |
Die über E berechneten Gesamtkosten (7,0) sind höher als die bisher hinterlegten Gesamtkosten (4,0). Das bedeutet: Wir konnten zwar einen neuen Weg zu F finden, allerdings ist dieser teurer als der bisher bekannte. Somit ignorieren wir ihn, d. h. wir lassen die Tabelleneinträge für Knoten F unverändert.
Die Tabelle sieht nun wie folgt aus (die Änderungen sind wieder fett markiert):
| Knoten | Vorgänger | Gesamtkosten vom Start | Minimale Restkosten zum Ziel | Summe aller Kosten |
|---|---|---|---|---|
| F | D | 4,0 | 1,5 | 5,5 |
| C | D | 3,0 | 3,2 | 6,2 |
| A | E | 4,0 | 3,9 | 7,9 |
| B | E | 6,0 | 4,3 | 10,3 |
| G | – | ∞ | 2,8 | ∞ |
| H | – | ∞ | 0,0 | ∞ |
| I | – | ∞ | 1,6 | ∞ |
Die neuen Einträge sind so lesen: Knoten A und B wurden entdeckt. Sie können über Knoten E in 4 bzw. 6 Minuten erreicht werden. Addiert man die minimalen Restkosten zum Ziel, ergeben sich 7,9 bzw. 10,3 Minuten, die man über die jeweiligen Knoten mindestens brauchen würde, um das Ziel zu erreichen. Diese Werte sind höher als die der Knoten F und C, weshalb die Knoten A und B in der Tabelle hinter F und C bleiben.
Schritt 3: Betrachten aller Nachbarn von Knoten F
Wir wiederholen das Ganze für Knoten F und betrachten dessen Nachbarn D, E und H:

Knoten D und E sind nicht mehr in der Tabelle. Wir haben die kürzesten Wege dorthin bereits entdeckt (in den vorangegangenen zwei Schritten).
Wir müssen also nur Knoten H betrachten. Wir berechnen, wie zuvor, die Gesamtkosten vom Start zu Knoten H:
| Knoten H | 4,0 (Gesamtkosten vom Start zu F) + 7,0 (Kosten F–H) = 11,0 |
Knoten H ist das Ziel. Daher existieren keine Restkosten, die wir noch addieren müssten. Wir tragen Vorgänger und Gesamtkosten ein:

Wir haben also einen Weg zum Zielknoten H gefunden. Dieser führt über Knoten F und hat Gesamtkosten von 11,0. Wir aktualisieren Knoten H in der Tabelle:
| Knoten | Vorgänger | Gesamtkosten vom Start | Minimale Restkosten zum Ziel | Summe aller Kosten |
|---|---|---|---|---|
| C | D | 3,0 | 3,2 | 6,2 |
| A | E | 4,0 | 3,9 | 7,9 |
| B | E | 6,0 | 4,3 | 10,3 |
| H | F | 11,0 | 0,0 | 11,0 |
| G | – | ∞ | 2,8 | ∞ |
| I | – | ∞ | 1,6 | ∞ |
In der Tabelle existieren noch drei Knoten mit einer Kostensumme von weniger als 11,0. Das bedeutet, dass wir über diese drei Knoten möglicherweise einen schnelleren Weg zum Ziel finden könnten. Wir müssen den Prozess so lange weiterführen, bis der Zielknoten die erste Position der Tabelle erreicht hat.
Schritt 4: Betrachten aller Nachbarn von Knoten C
Der nächste Knoten in der Tabelle ist Knoten C. Wir entfernen ihn und betrachten seine Nachbarn, A, D und G:

Knoten D (unser Startknoten) ist nicht mehr in der Tabelle.
Wir berechnen, wie schon zuvor, die Gesamtkosten vom Start über den aktuellen Knoten C zu den Knoten A und G:
| Knoten A | 3,0 (Gesamtkosten vom Start zu C) + 2,0 (Kosten C–A) = 5,0 |
| Knoten G | 3,0 (Gesamtkosten vom Start zu C) + 2,0 (Kosten C–G) = 5,0 |
Zu Knoten A hatten wir bereits einen Weg über E mit Gesamtkosten vom Start von 4 entdeckt. Die Gesamtkosten über den neuen Weg zu A sind mit 5 höher, wir ignorieren also den neu entdeckten Weg zu A.
Zu Knoten G hatten wir noch keinen Weg entdeckt. Zu den soeben berechneten Gesamtkosten vom Start addieren wir noch die vorab berechneten Restkosten zum Ziel:
| Knoten G | 5,0 (Gesamtkosten vom Start zu G) + 2,8 (minimale Restkosten von G zum Ziel) = 7,8 |
Wir tragen Vorgänger und Kosten für Knoten G in die Grafik ein:

Und wir aktualisieren Knoten G in der Tabelle:
| Knoten | Vorgänger | Gesamtkosten vom Start | Minimale Restkosten zum Ziel | Summe aller Kosten |
|---|---|---|---|---|
| G | C | 5,0 | 2,8 | 7,8 |
| A | E | 4,0 | 3,9 | 7,9 |
| B | E | 6,0 | 4,3 | 10,3 |
| H | F | 11,0 | 0,0 | 11,0 |
| I | – | ∞ | 1,6 | ∞ |
Knoten G ist in der Tabelle auf Platz eins vorgerückt. Der A*-Algorithmus geht nun also – mit Hilfe der Heuristik – davon aus, über Knoten G den schnellsten Weg zum Ziel zu finden.
(Dijkstras Algorithmus würde – aufgrund der niedrigeren Gesamtkosten vom Start – mit Knoten A fortfahren.)
Schritt 5: Betrachten aller Nachbarn von Knoten G
Wir entnehmen also Knoten G und betrachten dessen Nachbarn, C und H:

Knoten C ist nicht mehr in der Tabelle, diesen hatten wir im vorangegangenen Schritt abgearbeitet.
Wir berechnen die Gesamtkosten vom Start über Knoten G zu Knoten H:
| Knoten H | 5,0 (Gesamtkosten vom Start zu G) + 4,0 (Kosten G–H) = 9,0 |
Die aktuell in Knoten H hinterlegten Kosten betragen 11,0. Wir haben also über Knoten G einen schnelleren Weg zum Zielknoten H entdeckt. Wir aktualisieren Vorgänger und Kosten in Knoten H:

Restkosten existieren im Zielknoten keine.
Die aktualisierte Tabelle sieht wie folgt aus:
| Knoten | Vorgänger | Gesamtkosten vom Start | Minimale Restkosten zum Ziel | Summe aller Kosten |
|---|---|---|---|---|
| A | E | 4,0 | 3,9 | 7,9 |
| H | G | 9,0 | 0,0 | 9,0 |
| B | E | 6,0 | 4,3 | 10,3 |
| I | – | ∞ | 1,6 | ∞ |
Knoten A ist in der Tabelle noch vor dem Zielknoten. Die Summe aller Kosten in diesem Knoten ist mit 7,9 niedriger als die eben berechnete Kostensumme zu Knoten H. Das bedeutet: Würden es eine Luftlinienverbindung von Knoten A zum Ziel H geben, dann wäre der Weg über A schneller als der eben gefundene über G.
Im nächsten Schritt wird der Algorithmus herausfinden, ob es einen solchen Weg gibt oder nicht.
Schritt 6: Betrachten aller Nachbarn von Knoten A
Gehen wir es also an: Wir entnehmen Knoten A und betrachten dessen Nachbarn, C und E:

Beide Knoten sind nicht mehr in der Tabelle enthalten. Wir haben beide schon bearbeitet. Einen unentdeckten Weg zum Ziel finden wir in diesem Schritt also nicht.
Die Tabelle sieht nun so aus:
| Knoten | Vorgänger | Gesamtkosten vom Start | Minimale Restkosten zum Ziel | Summe aller Kosten |
|---|---|---|---|---|
| H | G | 9,0 | 0,0 | 9,0 |
| B | E | 6,0 | 4,3 | 10,3 |
| I | – | ∞ | 1,6 | ∞ |
Unser Zielknoten hat Platz 1 der Tabelle erreicht.
Schnellster Weg zum Ziel wurde gefunden
Das bedeutet: Es gibt keinen Knoten, über den ein noch kürzerer Weg zum Ziel gefunden werden könnte.
Auch nicht über Knoten B?
Die Gesamtkosten vom Start zu Knoten B betragen zwar nur 6,0, doch mit den minimalen Restkosten zum Ziel von 4,3 ergeben sich Gesamtkosten von mindestens 10,3, so dass der bisherige Bestwert 9,0 nicht mehr eingeholt werden kann.
Backtrace zur Bestimmung des vollständigen Weges
Aus der Tabelle können wir ablesen: Der Zielknoten H ist am schnellsten über Knoten G erreichbar. Doch wie bestimmen wir den vollständigen Weg vom Startknoten D zum Ziel? Hierzu führen wir einen sogenannten "Backtrace" durch: Wir beginnen beim Zielknoten und folgen allen Vorgängerknoten, bis wir den Startknoten erreichen.
Am einfachsten lässt sich das am Graph demonstrieren:

Der Vorgänger des Zielknotens H ist G; der Vorgänger von G ist C; und der Vorgänger von C ist der Startknoten D. Der schnellste Weg lautet also: D–C–G–H.
Unterschied A*-Algorithmus zu Dijkstras Algorithmus
Im letzten Schritt wurde der Unterschied zu Dijkstras Algorithmus noch einmal deutlich: Knoten B hat niedrigere Gesamtkosten vom Start (6) als Knoten H (9). Dijkstras Algorithmus würde an dieser Stelle noch prüfen müssen, ob das Ziel über Knoten B schneller erreicht werden könnte.
Durch die Heuristik weiß der A*-Algorithmus an dieser Stelle, dass die Gesamtkosten des Weges über Knoten B mindestens 10,3 betragen würden (Kosten vom Start 6,0 plus minimale Restkosten 4,3). Die Kosten des aktuellen Weges (9,0) sind also außer Reichweite.
Der A*-Algorithmus hat den schnellsten Weg zum Ziel somit in einem Schritt weniger gefunden als Dijkstras Algorithmus benötigt hätte. Wir werden später sehen, dass der Unterschied bei komplexeren Graphen (wie beispielsweise bei echten Straßenkarten) deutlich höher ausfallen wird.
A*-Algorithmus – Informelle Beschreibung
Vorbereitung:
- Erstelle eine Tabelle aller Knoten mit Vorgängerknoten, Gesamtkosten vom Start, minimalen Restkosten zum Ziel und Kostensumme.
- Setze die Gesamtkosten des Startknotens auf 0 und die aller anderer Knoten auf unendlich.
- Berechne über die Heuristik-Funktion die minimalen Restkosten zum Ziel für alle Knoten.
Abarbeitung der Knoten:
Solange die Tabelle nicht leer ist, entnehme das Element mit der kleinsten Kostensumme und mache damit folgendes:
- Ist das entnommene Element der Zielknoten? Wenn ja, ist die Abbruchbedingung erfüllt. Folge dann den Vorgängerknoten zurück zum Startknoten, um den kürzesten Weg zu bestimmen.
- Andersfalls betrachte alle Nachbarknoten des entnommenen Elements, die sich noch in der Tabelle befinden. Für jeden Nachbarknoten:
- Berechne die Gesamtkosten vom Start als Summe der Gesamtkosten vom Start zum entnommenen Knoten plus der Kosten vom entnommenen Knoten zum betrachteten Nachbarknoten.
- Sind die neu berechneten Gesamtkosten vom Start niedriger als die bisher gespeicherten? Wenn nein, dann ignoriere diesen Nachbarknoten. Wenn ja, dann:
- Berechne für den Nachbarknoten die Summe aus den soeben berechneten Gesamtkosten vom Start und den Restkosten zum Ziel.
- Trage als Vorgänger des Nachbarknotens den entnommenen Knoten ein.
- Trage für den Nachbarknoten die neu berechneten Gesamtkosten und die Kostensumme ein.
A*-Algorithmus – Java-Quellcode
Im folgenden zeige ich dir, Schritt für Schritt, wie man den A*-Algorithmus in Java implementiert und welche Datenstrukturen man dafür optimalerweise verwendet.
Den Code findest du im Paket eu.happycoders.pathfinding.astar in meinem GitHub-Repository.
Datenstruktur für die Knoten: NodeWithXYCoordinates
Zunächst brauchen wir eine Datenstruktur, die zu jedem Knoten die X- und Y-Koordinaten speichert (Klasse NodeWithXYCoordinates im GitHub-Repository):
public class NodeWithXYCoordinates implements Comparable<NodeWithXYCoordinates> {
private final String name;
private final double x;
private final double y;
// Constructur, getters, equals(), hashCode(), compareTo()
}Code-Sprache: Java (java)Die hier nicht mit abgedruckten Methoden equals(), hashCode() und compareTo() basieren auf dem Namen des Knoten.
Datenstruktur für den Graph: Guava ValueGraph
Als Datenstruktur für den Graph verwenden wir die Klasse ValueGraph der Google Core Libraries for Java. Diese stellt verschiedene Graph-Typen bereit, welche hier erläutert werden. Wir verwenden einen MutableValueGraph.
Der folgende Code zeigt, wie wir einen Graph erstellen, der dem aus dem Beispiel oben entspricht. Die X- und Y-Koordinaten habe ich aus der Grafik mit dem Koordinatensystem abgelesen. Die Einheit ist Meter; tatsächlich ist die Einheit aber irrelevant für das Finden des schnellsten Weges.
private static ValueGraph<NodeWithXYCoordinates, Double> createSampleGraph() {
MutableValueGraph<NodeWithXYCoordinates, Double> graph =
ValueGraphBuilder.undirected().build();
NodeWithXYCoordinates a = new NodeWithXYCoordinates("A", 2_410, 6_230);
NodeWithXYCoordinates b = new NodeWithXYCoordinates("B", 8_980, 6_080);
NodeWithXYCoordinates c = new NodeWithXYCoordinates("C", 560, 3_360);
NodeWithXYCoordinates d = new NodeWithXYCoordinates("D", 2_980, 3_900);
NodeWithXYCoordinates e = new NodeWithXYCoordinates("E", 4_220, 4_280);
NodeWithXYCoordinates f = new NodeWithXYCoordinates("F", 4_000, 2_600);
NodeWithXYCoordinates g = new NodeWithXYCoordinates("G", 0, 0);
NodeWithXYCoordinates h = new NodeWithXYCoordinates("H", 4_850, 110);
NodeWithXYCoordinates i = new NodeWithXYCoordinates("I", 7_500, 0);
graph.putEdgeValue(a, c, 2.0);
graph.putEdgeValue(a, e, 3.0);
graph.putEdgeValue(b, e, 5.0);
graph.putEdgeValue(b, i, 15.0);
graph.putEdgeValue(c, d, 3.0);
graph.putEdgeValue(c, g, 2.0);
graph.putEdgeValue(d, e, 1.0);
graph.putEdgeValue(d, f, 4.0);
graph.putEdgeValue(e, f, 6.0);
graph.putEdgeValue(f, h, 7.0);
graph.putEdgeValue(g, h, 4.0);
graph.putEdgeValue(h, i, 3.0);
return graph;
}Code-Sprache: Java (java)Die Typparameter des ValueGraph sind:
- Typ der Knoten: im Beispiel
NodeWithXYCoordinatesfür die Knoten mitsamt ihren X- und Y-Koordinaten - Typ der Kantenwerte: im Beispiel
Doublefür die Kosten zwischen zwei Knoten
Der Graph ist ungerichtet; es spielt also keine Rolle, in welcher Reihenfolge wir die Knoten in der putEdgeValue()-Methode angeben.
Heuristik-Funktion: HeuristicForNodesWithXYCoordinates
Die Heuristik-Funktion muss zu einem gegebenen Knoten die minimalen Restkosten zum Ziel berechnen können. Es bietet sich an das Function-Interface zu implementieren (im GitHub-Repository findest du die Klasse HeuristicForNodesWithXYCoordinates mit zusätzlichen Kommentaren und Debug-Ausgaben):
public class HeuristicForNodesWithXYCoordinates
implements Function<NodeWithXYCoordinates, Double> {
private final double maxSpeed;
private final NodeWithXYCoordinates target;
public HeuristicForNodesWithXYCoordinates(
ValueGraph<NodeWithXYCoordinates, Double> graph, NodeWithXYCoordinates target) {
this.maxSpeed = calculateMaxSpeed(graph);
this.target = target;
}
private static double calculateMaxSpeed(
ValueGraph<NodeWithXYCoordinates, Double> graph) {
return graph.edges().stream()
.map(edge -> calculateSpeed(graph, edge))
.max(Double::compare)
.get();
}
private static double calculateSpeed(
ValueGraph<NodeWithXYCoordinates, Double> graph,
EndpointPair<NodeWithXYCoordinates> edge) {
double euclideanDistance = calculateEuclideanDistance(edge.nodeU(), edge.nodeV());
double cost = graph.edgeValue(edge).get();
double speed = euclideanDistance / cost;
return speed;
}
public static double calculateEuclideanDistance(
NodeWithXYCoordinates source, NodeWithXYCoordinates target) {
double distanceX = target.getX() - source.getX();
double distanceY = target.getY() - source.getY();
return Math.sqrt(distanceX * distanceX + distanceY * distanceY);
}
@Override
public Double apply(NodeWithXYCoordinates node) {
double euclideanDistance = calculateEuclideanDistance(node, target);
double minimumCost = euclideanDistance / maxSpeed;
return minimumCost;
}
}Code-Sprache: Java (java)Dem Konstrukor werden der Graph und der Zielknoten übergeben. In der Methode calculateMaxSpeed() wird für alle Kanten die Geschwindigkeit und davon das Maximum bestimmt. Maximalgeschwindigkeit und Zielknoten werden in Instanzvariablen gespeichert.
In der apply()-Methode wird letztendlich die Heuristik auf den übergebenen Knoten angewendet: Es wird die euklidische Distanz zum Zielknoten berechnet und diese durch die Maximalgeschwindigkeit geteilt, um die minimalen Restkosten vom übergebenen Knoten zum Ziel zu berechnen.
Datenstruktur: Tabelleneinträge
Für die Tabelle der Knoten benötigen wir eine Datenstruktur, in der wir zu jedem Knoten dessen Vorgänger speichern, sowie die Gesamtkosten vom Start, die minimalen Restkosten zum Ziel und die Kostensumme. Der folgende Code zeigt die dafür implementierte Klasse AStarNodeWrapper:
public class AStarNodeWrapper<N extends Comparable<N>>
implements Comparable<AStarNodeWrapper<N>> {
private final N node;
private AStarNodeWrapper<N> predecessor;
private double totalCostFromStart;
private final double minimumRemainingCostToTarget;
private double costSum;
public AStarNodeWrapper(
N node,
AStarNodeWrapper<N> predecessor,
double totalCostFromStart,
double minimumRemainingCostToTarget) {
this.node = node;
this.predecessor = predecessor;
this.totalCostFromStart = totalCostFromStart;
this.minimumRemainingCostToTarget = minimumRemainingCostToTarget;
calculateCostSum();
}
private void calculateCostSum() {
this.costSum = this.totalCostFromStart + this.minimumRemainingCostToTarget;
}
// getter for node
// getters and setters for predecessor
public void setTotalCostFromStart(double totalCostFromStart) {
this.totalCostFromStart = totalCostFromStart;
calculateCostSum();
}
// getter for totalCostFromStart
@Override
public int compareTo(AStarNodeWrapper<N> o) {
int compare = Double.compare(this.costSum, o.costSum);
if (compare == 0) {
compare = node.compareTo(o.node);
}
return compare;
}
// equals(), hashCode()
}Code-Sprache: Java (java)Der Typparameter N steht für den Typ der Knoten – in unserem Beispiel wird das NodeWithXYCoordinates sein. Die Parametrisierung erlaubt es uns auch andere Typen zu verwenden, z. B. einen Knoten mit Längen- und Breitengraden – oder einen mit zusätzlicher Z-Koordinate).
Im Konstruktor sowie in der Methode setTotalCostFromStart() wird calculateCostSum() aufgerufen, um die Summe aus Gesamtkosten vom Start und minimalen Restkosten zum Ziel zu berechnen.
Diese Summe wird wiederum in der compareTo()-Methode verwendet, um die natürliche Ordnung der Wrapper-Klasse so zu definieren, dass diese nach Kostensumme aufsteigend sortiert wird. Bei gleicher Kostensumme werden die Knoten selbst verglichen. Im Fall von NodeWithXYCoordinates würde dann nach Knotenname sortiert werden. (Warum der zweite Vergleich bei gleicher Kostensumme unbedingt nötig ist, wirst du weiter unten erfahren.)
Datenstruktur: TreeSet als Tabelle
Wer den Artikel über Dijkstras Algorithmus gelesen hat, weiß, dass die in Pathfinding-Tutorials häufig eingesetzte PriorityQueue nicht die optimale Datenstruktur für diese Tabelle ist. Warum das so ist, werde ich im Abschnitt über die Zeitkomplexität noch einmal zeigen. Wir verwenden stattdessen ein TreeSet.
Das TreeSet liefert mit der pollFirst()-Methode das kleinste Elemente zurück. Durch die oben beschriebene natürliche Ordnung der AStarNodeWrapper-Objekte wird dies immer der Knoten mit der geringsten Summe aus Gesamtkosten vom Start und minimalen Restkosten zum Ziel sein.
TreeSet<AStarNodeWrapper<N>> queue = new TreeSet<>();Code-Sprache: GLSL (glsl)Datenstruktur: Lookup Map für Wrapper
Im weiteren Verlauf benötigen eine Map, die für einen Knoten des Graphen den dazugehörigen Wrapper liefert. Hierfür verwenden wir eine HashMap:
Map<N, AStarNodeWrapper<N>> nodeWrappers = new HashMap<>();Code-Sprache: GML (gml)Datenstruktur: Abgearbeitete Knoten
Um prüfen zu können, ob wir einen Knoten bereits abgearbeitet haben, d. h. den kürzesten Weg dorthin gefunden haben, legen wir ein HashSet an:
Set<N> shortestPathFound = new HashSet<>();Code-Sprache: Java (java)Vorbereitung: Füllen der Tabelle
Kommen wir zum vorbereitenden Schritt, dem Füllen der Tabelle.
An dieser Stelle können wir eine Optimierung gegenüber der informellen Beschreibung des Algorithmus vornehmen. Anstatt alle Knoten in die Tabelle zu schreiben, schreiben wir zunächst nur den Startknoten. Alle weiteren Knoten fügen wir erst dann in die Tabelle ein, wenn wir einen Weg dorthin gefunden haben.
Hierdurch schlagen wir drei Fliegen mit einer Klappe:
- Wir sparen Tabelleneinträge für diejenigen Knoten, die vom Startpunkt aus nicht erst erreichbar sind oder nur über solche Zwischenknoten, deren Kostensumme höher ist als die Kosten eines bereits gefundenen Weges (wie im Beispiel der Knoten I).
- Auf ebendiese Knoten brauchen wir auch die Heuristik-Funktion nicht anzuwenden.
- Wenn wir die Kostensumme eines Knotens, der sich bereits in der Tabelle befindet, neu berechnen, müssen wir den Knoten aus der Tabelle entfernen und ihn neu einfügen, damit er an die richtige Position sortiert wird. Auch diesen Mehraufwand sparen wir uns, wenn wir die Knoten erst dann einfügen, wenn wir einen Weg dorthin entdeckt haben.
Wir beginnen also damit unseren Startknoten in einen AStarNodeWrapper einzupacken – und fügen diesen in Lookup-Map und Tabelle ein:
AStarNodeWrapper<N> sourceWrapper =
new AStarNodeWrapper<>(source, null, 0.0, heuristic.apply(source));
nodeWrappers.put(source, sourceWrapper);
queue.add(sourceWrapper);Code-Sprache: Java (java)Iteration über alle Knoten
Die folgende Schleife implementiert die schrittweisen Abarbeitung der Knoten (Methode findShortestPath() in der Klasse AStarWithTreeSet):
while (!queue.isEmpty()) {
AStarNodeWrapper<N> nodeWrapper = queue.pollFirst();
N node = nodeWrapper.getNode();
shortestPathFound.add(node);
// Have we reached the target? --> Build and return the path
if (node.equals(target)) {
return buildPath(nodeWrapper);
}
// Iterate over all neighbors
Set<N> neighbors = graph.adjacentNodes(node);
for (N neighbor : neighbors) {
// Ignore neighbor if shortest path already found
if (shortestPathFound.contains(neighbor)) {
continue;
}
// Calculate total cost from start to neighbor via current node
double cost =
graph.edgeValue(node, neighbor).orElseThrow(IllegalStateException::new);
double totalCostFromStart = nodeWrapper.getTotalCostFromStart() + cost;
// Neighbor not yet discovered?
AStarNodeWrapper<N> neighborWrapper = nodeWrappers.get(neighbor);
if (neighborWrapper == null) {
neighborWrapper =
new AStarNodeWrapper<>(
neighbor, nodeWrapper, totalCostFromStart, heuristic.apply(neighbor));
nodeWrappers.put(neighbor, neighborWrapper);
queue.add(neighborWrapper);
}
// Neighbor discovered, but total cost via current node is lower?
// --> Update total cost and predecessor
else if (totalCostFromStart < neighborWrapper.getTotalCostFromStart()) {
// The position in the TreeSet won't change automatically;
// we have to remove and reinsert the node.
// Because TreeSet uses compareTo() to identity a node to remove,
// we have to remove it *before* we change the cost!
queue.remove(neighborWrapper);
neighborWrapper.setTotalCostFromStart(totalCostFromStart);
neighborWrapper.setPredecessor(nodeWrapper);
queue.add(neighborWrapper);
}
}
}
// All nodes were visited but the target was not found
return null;Code-Sprache: Java (java)Den Code versteht man am besten, wenn man ihn sich Block für Block mitsamt der Kommentare anschaut.
Backtrace: Bestimmung des Weges vom Start zum Ziel
In dem mit "Have we reached the target?" kommentierten if-Block wird die Methode buildPath() aufgerufen. Diese folgt den Vorgängern vom Zielknoten zurück zum Startknoten, trägt dabei alle Knoten in eine Liste ein und gibt diese in umgekehrter Reihenfolge zurück:
private static <N extends Comparable<N>> List<N> buildPath(
AStarNodeWrapper<N> nodeWrapper) {
List<N> path = new ArrayList<>();
while (nodeWrapper != null) {
path.add(nodeWrapper.getNode());
nodeWrapper = nodeWrapper.getPredecessor();
}
Collections.reverse(path);
return path;
}Code-Sprache: Java (java)Die vollständige findShortestPath()-Methode findest Du in der Klasse AStarWithTreeSet im GitHub-Repository. Aufrufen kannst Du die Methode dann beispielsweise so:
ValueGraph<NodeWithXYCoordinates, Double> graph = createSampleGraph();
Map<String, NodeWithXYCoordinates> nodeByName = createNodeByNameMap(graph);
Function<NodeWithXYCoordinates, Double> heuristic =
new HeuristicForNodesWithXYCoordinates(graph, target);
List<NodeWithXYCoordinates> shortestPath =
AStarWithTreeSet.findShortestPath(
graph, nodeByName.get("D"), nodeByName.get("H"), heuristic);Code-Sprache: Java (java)Dieses und andere Beispiele findest du in der Klasse TestWithSampleGraph im GitHub-Repository.
Kommen wir nun zur Zeitkomplexität.
Zeitkomplexität des A*-Algorithmus
Zur Bestimmung der Zeitkomplexität des A*-Algorithmus schauen wir uns den Code Block für Block an, bestimmen für jeden Block die Teilkomplexität und addieren diese im Anschluss.
Wir bezeichnen dabei die Anzahl der Knoten des Graphes mit n und die Anzahl der Kanten mit m.
Die Berechnung der maximalen Geschwindigkeit im Graphen brauchen wir hier nicht zu berücksichtigen, da diese pro Graph nur einmalig erfolgen muss und dann als Teil der Graphdaten gespeichert werden kann.
- Einfügen des Startknotens in die Tabelle: Der Aufwand ist unabhängig von der Größe des Graphen, also konstant – O(1).
- Entnehmen der Knoten aus der Tabelle: Der Aufwand für das Entnehmen des kleinsten Elements der Tabelle ist abhängig von der verwendeten Datenstruktur – wir bezeichnen ihn mit Tem ("extract minimum"). Jeder Knoten wird maximal einmal entnommen, die Komplexität beträgt also O(n · Tem).
- Prüfen, ob der kürzeste Pfad zu einem Knoten bereits gefunden wurde: Für jeden Knoten im Graph erfolgt diese Prüfung maximal einmal für alle angrenzenden Knoten. Die Anzahl der angrenzenden Knoten entspricht der Anzahl von wegführenden Kanten. Da jede Kante genau an zwei Knoten angrenzt, gibt es doppelt so viele wegführende Kanten wie Knoten, also 2 · m. Für die Prüfung verwenden wir ein Set, sie erfolgt also in konstanter Zeit. Insgesamt kommen wir also auf eine Komplexität von O(2 · m) = O(m).
- Berechnung der Gesamtkosten vom Start: Die Berechnung ist eine einfache Addition und hat damit den Aufwand O(1). Die Berechnung erfolgt maximal einmal pro Kante, da wir jeder Kante maximal einmal folgen. Die Komplexität ist also auch für diesen Block O(m).
- Zugriff auf NodeWrapper: Der Zugriff auf die Lookup-Map für NodeWrapper erfolgt jeweils nach Berechnung der Gesamtkosten. Der Zugriff ist ebenfalls konstant, die Komplexität für diesen Schritt also auch O(m).
- Berechnung der Heuristik: Die Heuristik-Funktion ist mit konstantem Aufwand berechenbar. Sie muss maximal einmal pro Knoten durchgeführt werden. Die Komplexität beträgt also O(n).
- Einfügen in die Tabelle: Der Aufwand für das Einfügen ist – genau wie der Aufwand für das Entnehmen – abhängig von der verwendeten Datenstruktur. Wir bezeichnen ihn mit Ti ("insert"). Jeder Knoten wird maximal einmal eingefügt. Die Komplexität beträgt demnach O(n · Ti).
- Aktualisieren der Gesamtkosten und damit der Kostensumme in der Tabelle: Auch dieser Aufwand hängt von der Datenstruktur ab. Beim
TreeSetbeispielsweise mussten wir den Knoten entnehmen und wieder einfügen. Andere Datenstrukturen (eine wirst du gleich kennenlernen) haben eine eigenständige Funktion hierfür. Wir bezeichnen den Aufwand allgemein mit Tdk ("decrease key"). Die Funktion wird maximal so oft aufgerufen wie wir die Gesamtkosten vom Start berechnen, also maximal m mal. Die Komplexität für diesen Block lautet also O(m · Tdk).
Wir addieren alle Teilkomplexitäten:
O(1) + O(n · Tem) + O(m) + O(m) + O(m) + O(n · Ti) + O(n) + O(m · Tdk)
Konstanter Aufwand O(1) kann vernachlässigt werden; ebenso sind O(m) gegenüber O(m · Tdk) vernachlässigbar und O(n) gegenüber O(n · Tem) und O(n · Ti). Wir können den Term daher kürzen zu O(n · Tem) + (n · Ti) + O(m · Tdk) und dann weiter zusammenfassen zu:
O(n · (Tem+Ti) + m · Tdk)
In den folgenden Abschnitten schauen wir uns an, was die Werte für Tem, Ti und Tdk für die verschiedenen Datenstrukturen sind – und was sich daraus für Gesamtkomplexitäten ergeben.
A*-Algorithmus mit TreeSet
Das im Quellcode verwendete TreeSet hat folgenden Komplexitäten (diese können der TreeSet-Dokumentation entnommen werden). Für ein besseres Verständnis gebe ich die T-Werte hier mit voller Bezeichnung an:
- Kleinsten Eintrag entnehmen mit
pollFirst(): TextractMinimum = O(log n) - Wert einfügen mit
add(): Tinsert = O(log n) - Kosten verringen mit
remove()undadd(): TdecreaseKey = O(log n) + O(log n) = O(log n)
Wir setzen diese Werte in die allgemeine Formel des vorherigen Abschnitts ein und erhalten:
O(n · log n + m · log n)
Für den Sonderfall, dass die Anzahl der Kanten ein Vielfaches der Anzahl der Knoten ist – in Landau-Notation: m ∈ O(n) – können wir m und n bei der Berechnung der Zeitkomplexität gleichsetzen.
Die Formel vereinfacht sich dann zu:
O(n · log n) – für m ∈ O(n)
Der Aufwand ist also quasilinear.
Bei der Verwendung von TreeSet ist zu beachten, dass dieses die Interface-Definition der remove()-Methode der Collection- und Set-Interfaces verletzt, da es das zu löschende Element nicht anhand der equals()-Methode identifiziert, sondern über die compareTo()-Methode. Es muss also sichergestellt sein, dass die compareTo()-Methode der verwendeten Knotenklasse dann – und nur dann – 0 zurückliefert, wenn auch die equals()-Methode true ergibt.
Laufzeit mit TreeSet
Mit dem Programm TestAStarRuntime können wir messen, wie lange der A*-Algorithmus benötigt, um in Graphen verschiedener Größen den kürzesten Weg zwischen zwei Punkten zu finden. Das Programm generiert zufällige Graphen und misst dann die Ausführungszeit von AStarWithTreeSet.findShortestPath().
Für jede Graphengröße werden 50 Tests mit unterschiedlichen Graphen durchgeführt und schließlich der Median der Messwerte ausgegeben. Das folgende Diagramm zeigt die Messungen der Laufzeit im Verhältnis zur Graphengröße für das TreeSet:

Das vorhergesagte quasilineare Wachstum ist einigermaßen gut zu erkennen.
A*-Algorithmus mit PriorityQueue
Bei der Auswahl der Datenstruktur hatte ich bereits die gerne eingesetzte PriorityQueue angesprochen. Warum ist diese keine gute Wahl?
Die Komplexitäten entnehmen wir wieder direkt dem PriorityQueue-JavaDoc:
- Kleinsten Eintrag entnehmen mit
poll(): TextractMinimum = O(log n) - Wert einfügen mit
offer(): Tinsert = O(log n) - Kosten verringen mit
remove()undoffer(): TdecreaseKey = O(n) + O(log n) = O(n)
Die ersten zwei Parameter, Tem und Ti gleichen denen des TreeSets.
Der dritte Parameter, Tdk hingegen ist bei der PriorityQueue allerdings O(n) – im Gegensatz zum deutlich günstigeren O(log n) beim TreeSet.
Was bedeutet das für die Zeitkomplexität des A*-Algorithmus? Wir tragen die Parameter in die allgemeine Formel O(n · (Tem+Ti) + m · Tdk) ein und erhalten:
O(n · (log n + log n) + m · n)
log n + log n ist 2 · log n, und Konstanten können wir weglassen. Der Term verkürzt sich somit auf:
O(n · log n + m · n)
Für den Sonderfall m ∈ O(n) (die Anzahl der Kanten ist ein Vielfaches der Anzahl der Knoten), können wir die Formel vereinfachen zu O(n · log n + n²). Neben dem quadratischen Anteil n² können wir den quasilinearen Anteil n · log n vernachlässigen. Es bleibt:
O(n²) – für m ∈ O(n)
Der Einsatz einer PriorityQueue führt also zu quadratischem Aufwand, einer deutlich schlechteren Komplexitätsklasse als quasilinearer Aufwand.
Laufzeit mit PriorityQueue
Wenn wir im Programm TestAStarRuntime in Zeile 79 die Klasse AStarWithTreeSet durch AStarWithPriorityQueue (Klasse in GitHub) ersetzen, können wir die Laufzeiten unter Verwendung der PriorityQueue messen.
Das folgende Diagramm zeigt das Messergebnis:

Das quadratische Wachstum ist sehr gut zu erkennen.
A*-Algorithmus mit Fibonacci-Heap
Es gibt eine noch besser geeignete Datenstruktur: den Fibonacci-Heap. Dieser garantiert folgende Laufzeiten:
- Kleinsten Eintrag entnehmen: TextractMinimum = O(log n)
- Wert einfügen: Tinsert = O(1)
- Kosten verringen: TdecreaseKey = O(1)
Hier haben wir also zwei Anteile mit konstantem Aufwand. Setzen wir die Parameter in die allgemeine Formel O(n · (Tem+Ti) + m · Tdk) ein:
O(n · log n + m)
Für den Sonderfall m ∈ O(n) vereinfacht sich die Formel auf:
O(n · log n) – für m ∈ O(n)
In Bezug auf die Zeitkomplexität des Gesamtalgorithmus bringt uns der Fibonacci-Heap keinen Vorteil. Wie sieht die Laufzeit in der Praxis aus?
Laufzeit mit Fibonacci-Heap
Das JDK enthält leider keinen Fibonacci-Heap. Stattdessen verwende ich die Fibonacci-Heap-Implementierung von Keith Schwarz.
Diese Klasse und die entsprechende A*-Implementierung habe ich aus Copyright-Gründen nicht in mein Repository kopiert. Du kannst die Klasse unter dem angegebenen Link herunterladen und zur Übung selbst eine AStarWithFibonacciHeap-Klasse schreiben.
Mit dem Fibonacci-Heap erhalte ich folgende Messergebnisse:

Der A*-Algorithmus ist also mit dem FibonacciHeap noch einmal leicht schneller als mit dem TreeSet.
Zeitkomplexität – Zusammenfassung
Die folgende Tabelle zeigt zusammengefasst die Zeitkomplexität des A*-Algorithmus in Abhängigkeit von der eingesetzten Datenstruktur:
| Datenstruktur | Tem | Ti | Tdk | Zeitkomplexität allgemein | Zeitkomplexität für m ∈ O(n) |
|---|---|---|---|---|---|
| PriorityQueue | O(log n) | O(log n) | O(n) | O(n · log n + m · n) | O(n²) |
| TreeSet | O(log n) | O(log n) | O(log n) | O(n · log n + m · log n) | O(n · log n) |
| FibonacciHeap | O(log n) | O(1) | O(1) | O(n · log n + m) | O(n · log n) |
Zeitkomplexität A*-Algorithmus vs. Dijkstras Algorithmus
Die Zeitkomplexitätsklassen bei A* sind die gleichen wie bei Dijkstra. Doch wie sieht es mit der Laufzeit aus?
Im folgenden Diagramm siehst du zusätzlich zu den oben gemessenen Laufzeiten diejenigen des Dijkstra-Algorithmus aus dem vorherigen Artikel:

Die Laufzeiten sind beim A*-Algorithmus also deutlich besser (zwischen Faktor 2 und 4). Dies ist allerdings keine allgemeingültige Aussage. Ob und inwieweit A* schneller ist als Dijkstra hängt stark von der Struktur des Graphen ab. Für Straßenkarten ist A* in der Regel deutlich schneller.
In einem Labyrinth, in dem der kürzeste Weg oft nicht in die direkte Richtung zum Ziel führt, kann das ganz anders aussehen.
Zusammenfassung und Ausblick
Dieser Artikel hat an einem Beispiel, mit einer informellen Beschreibung und mit Java-Quellcode gezeigt, wie der A*-Algorithmus funktionert.
Für die Zeitkomplexität haben wir zunächst eine allgemeine Landau-Notation hergeleitet und diese anschließend für die Datenstrukturen TreeSet, PriorityQueue und FibonacciHeap konkretisiert.
Die Zeitkomplexitäten entsprechen denen des Dijkstra-Algorithmus; die Laufzeiten sind bei A* deutlich besser als bei Dijkstra. Wenn eine Heuristik-Funktion definiert werden kann und der schnellste Weg in der Regel grob in die Richtung des Ziels führt, ist also immer der A*-Algorithmus vorzuziehen.
Vorschau: Bellman-Ford-Algorithmus
Es gibt allerdings auch Situationen, in denen weder Dijkstra noch A* ein geeigneter Algorithmus sind: Wenn es Kanten mit negativen Gewichten gibt, würden Dijkstra und A* diese ignorieren, wenn diese auf einen Knoten folgen würden, zu dem die Kosten höher sind als die eines bereits entdeckten Weges zum Ziel.
Wie negative Kantengewichte in der Realität (und nicht nur in einem konstruierten mathematischen Modell) überhaupt existieren können – und wie man das Kürzeste-Wege-Problem in so einem Fall löst, erfährst Du im nächsten Artikel über den Bellman-Ford-Algorithmus.
