

In der Artikelserie über Sortieralgorithmen kommem wir nach drei relativ leicht zu verstehenden Sortierverfahren (Insertion Sort, Selection Sort, Bubble Sort) zu den komplexeren – dafür aber auch deutlich effizienteren Algorithmen.
Wir beginnen mit Quicksort ("Sort" ist hier kein separates Wort, also nicht "Quick Sort"). Dieser Artikel:
- beschreibt den Quicksort-Algorithmus,
- zeigt dessen Quellcode in Java,
- erklärt, wie man die Zeitkomplexität von Quicksort herleitet,
- testet, ob die Performance der Java-Implementierung mit dem erwarteten Laufzeitverhalten übereinstimmt,
- stellt mehrere Algorithmus-Optimierungen vor (Kombination mit Insertion Sort und Dual-Pivot Quicksort)
- und misst und vergleicht auch deren Geschwindigkeit.
Die Quellcodes der Artikelserie findest du in meinem GitHub-Repository.
Quicksort Algorithmus
Quicksort funktioniert nach dem "Teile-und-herrsche"-Prinzip ("divide and conquer"):
Als erstes teilen wir die zu sortierenden Elemente auf zwei Bereiche auf – einen mit kleinen Elementen (im folgenen Beispiel "A") und einen mit großen Elementen (im Beispiel "B").
Welche Elemente klein sind und welche groß, entscheidet dabei das sogenannte Pivot-Element. Das Pivot-Element kann ein beliebiges Element aus dem Eingabe-Array sein. (Welches man wählt, bestimmt die Pivot-Strategie, dazu später mehr.)
Das Array wird nun so umsortiert, dass
- die Elemente, die kleiner als das Pivot-Element sind, im linken Bereich landen,
- die Elemente, die größer als das Pivot-Element sind, im rechten Bereich landen,
- und dass das Pivot-Element zwischen den zwei Bereichen positioniert wird – und damit automatisch an seiner endgültigen Position.
In folgendem Beispiel werden die Elemente [3, 7, 1, 8, 2, 5, 9, 4, 6] auf diese Art umsortiert. Als Pivot-Element habe ich das letzte Element des unsortierten Eingabe-Arrays gewählt (die orange gefärbte 6):
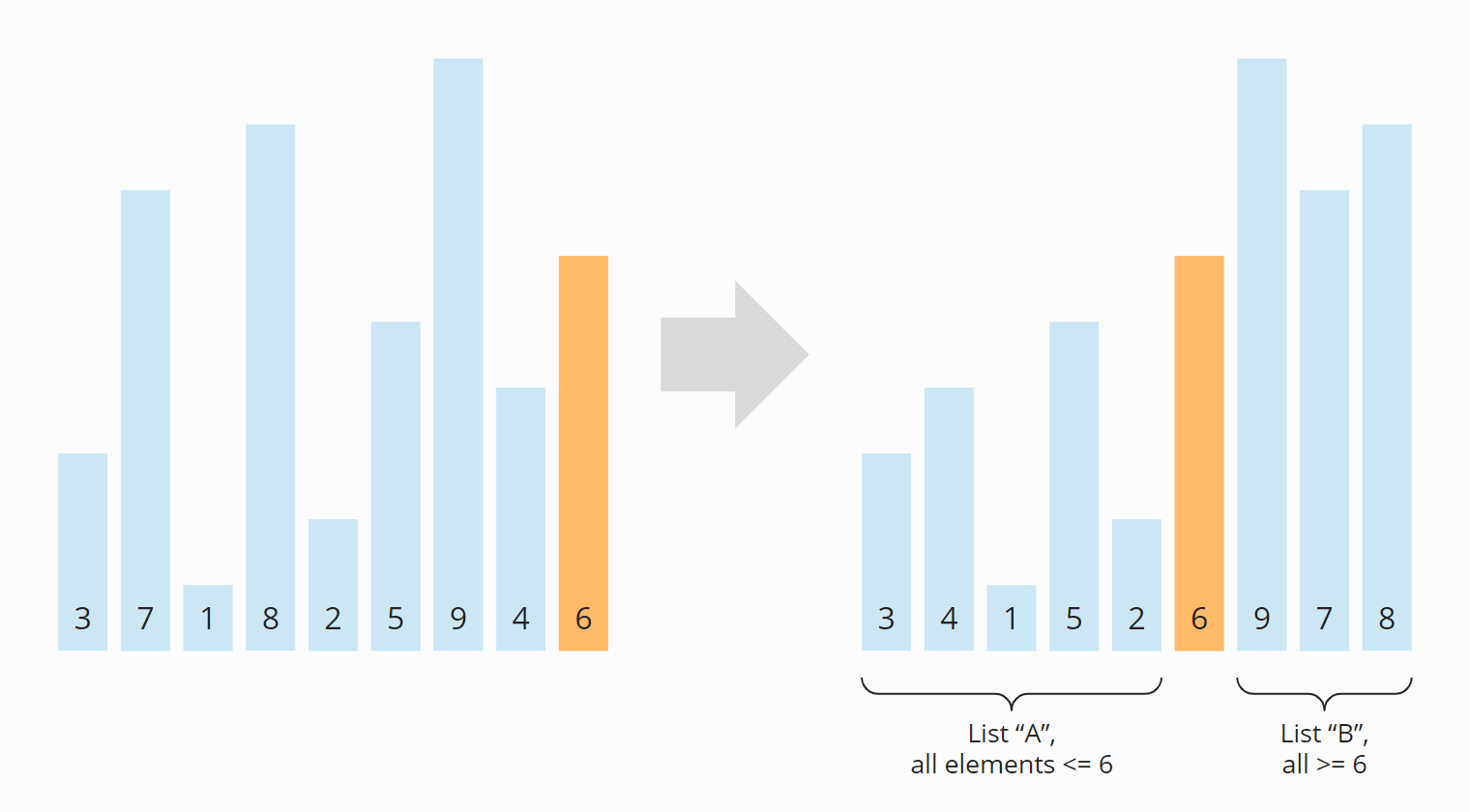
Dieses Aufteilen auf zwei Teil-Arrays nennt man Partitionieren. Wie die Partitionierung genau funktioniert, erfährst du im nächsten Abschnitt. Vorher zeige ich dir, wie der übergeordnete Algorithmus weitergeht.
Die Teil-Arrays links und rechts des Pivot-Elements sind nach der Partitionierung weiterhin unsortiert. Die Teil-Arrays werden nun ebenfalls partitioniert. Das Pivot-Element aus dem vorherigen Schritt, die 6, habe ich halbtransparent dargestellt, um die zwei Teil-Arrays besser erkennen zu können:
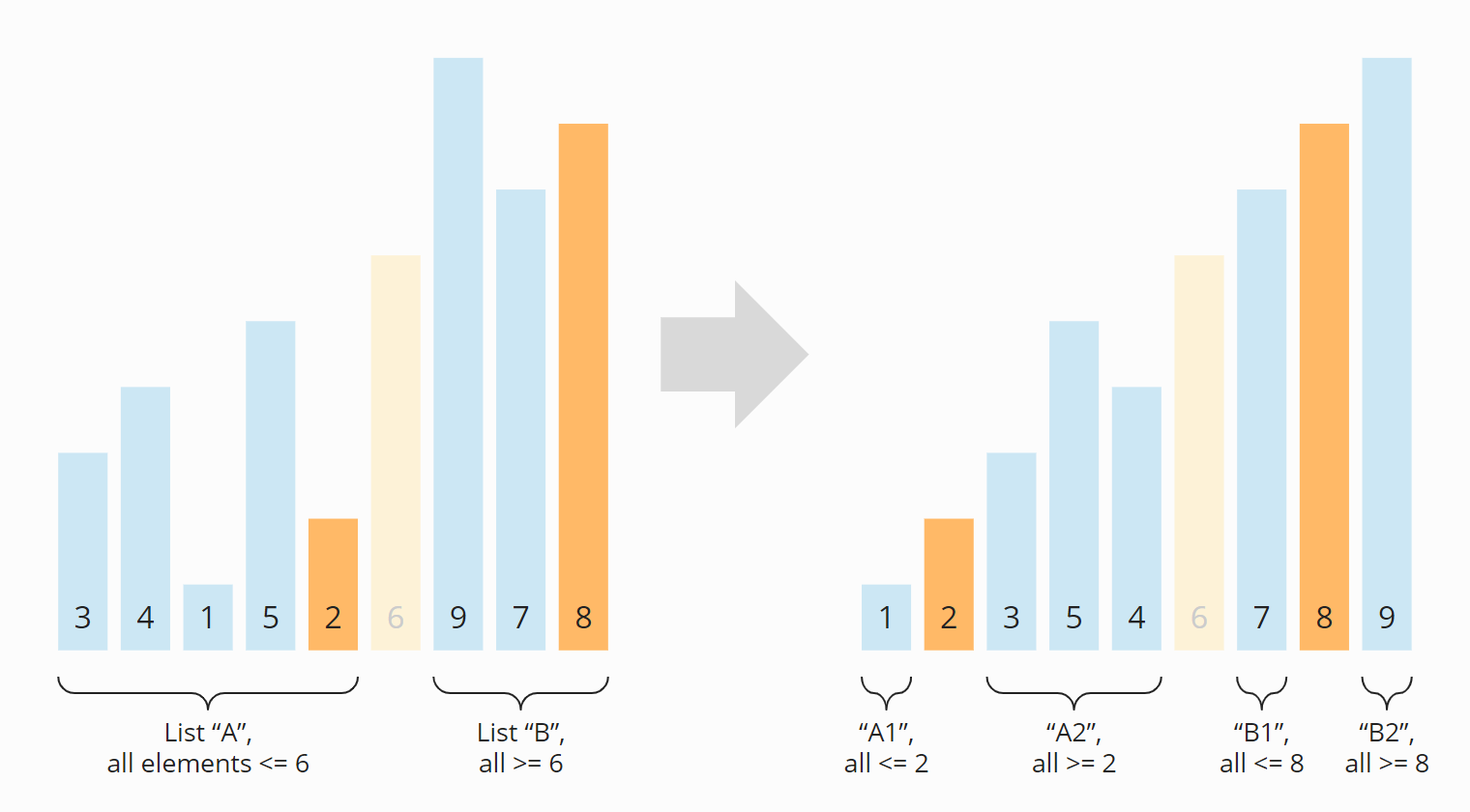
Nach der erneuten Partitionierung haben wir vier Bereiche: Aus A sind A1 und A2 entstanden; aus B sind B1 und B2 hervorgegangen. Die Bereiche A1, B1 und B2 bestehen aus nur noch einem Element und gelten damit als sortiert ("beherrscht" im Sinne von "Teile und herrsche"). Jetzt müssen wir nur noch das Teil-Array A2 partitionieren:
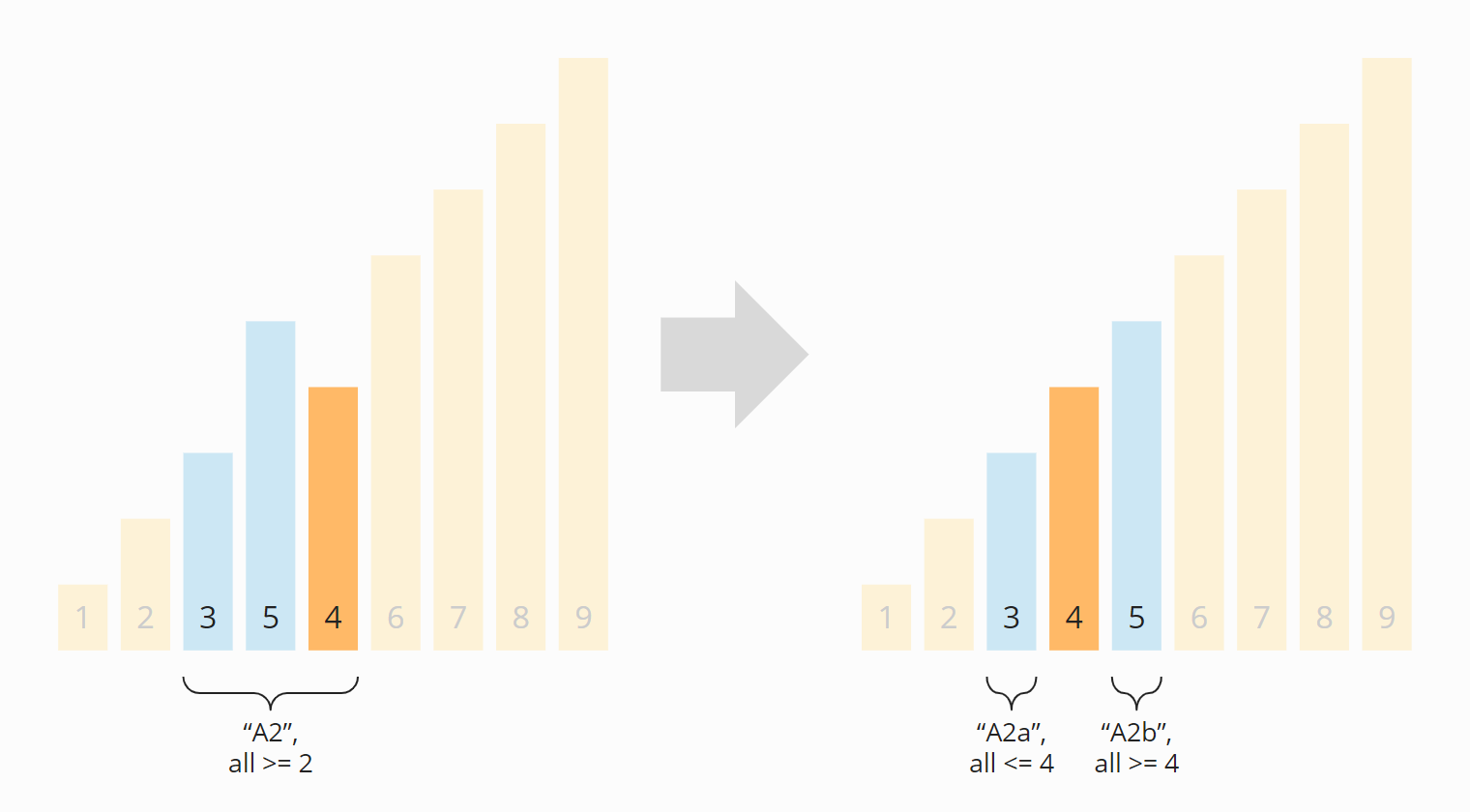
Die zwei in diesem Schritt aus A2 entstandenen Partitionen A2a und A2b haben wieder die Länge 1 und gelten damit als sortiert. Somit sind alle Teil-Arrays sortiert – und damit auch das gesamte Array:
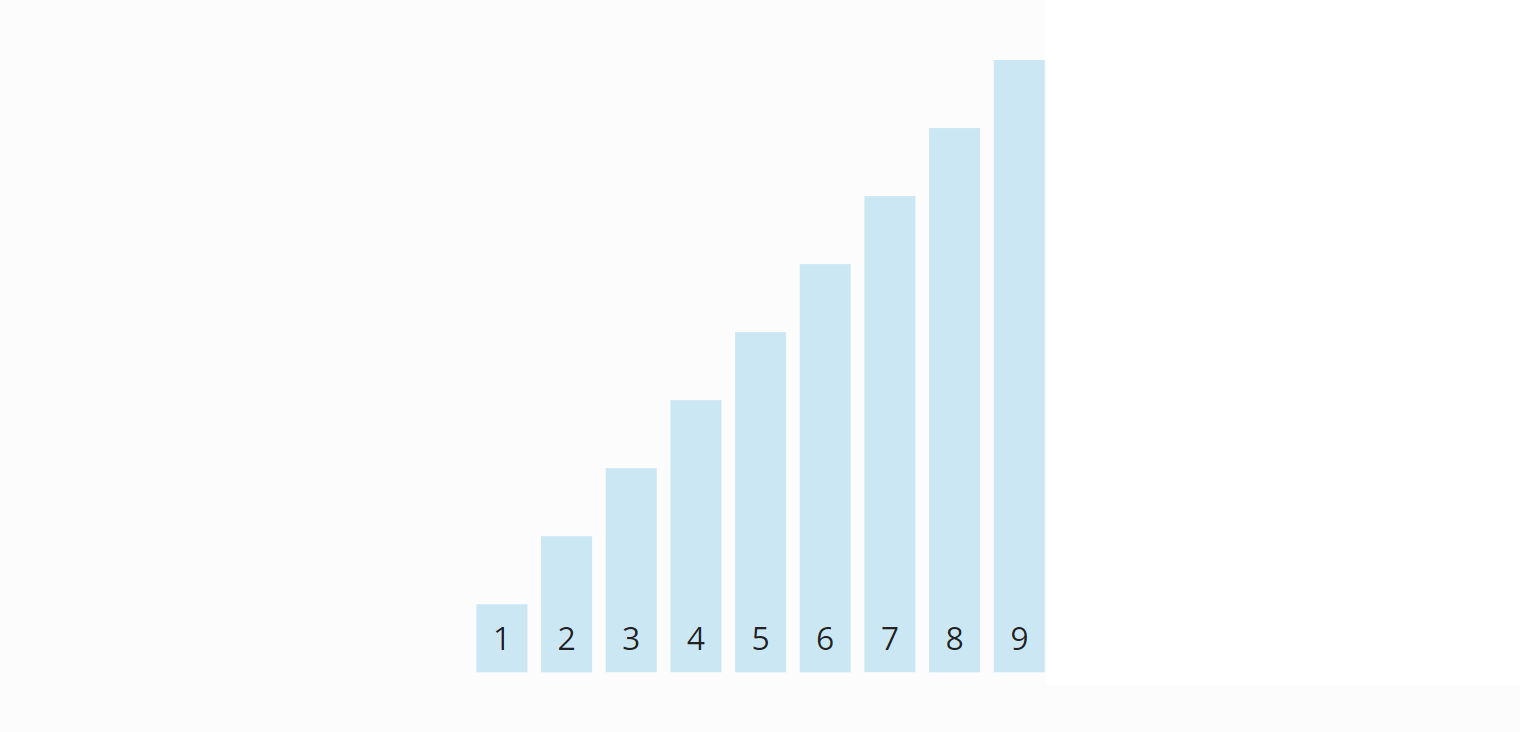
Der Algorithmus ist damit beendet.
Wie die Aufteilung eines Arrays in zwei Bereiche funktioniert – die Partitionierung – erkläre ich im nächsten Abschnitt.
Quicksort Partitionierung
Die Aufteilung des Arrays in zwei Partitionen erfolgt, in dem wir von links beginnend nach Elementen suchen, die größer als das Pivot-Element sind, und von rechts beginnend nach Elementen, die kleiner sind als das Pivot-Element.
Diese Elemente werden dann jeweils vertauscht. Dies wiederholen wir solange, bis die linke und rechte Suchposition aufeinander getroffen oder aneinander vorbeigelaufen sind.
Im Beispiel von oben funktioniert das wie folgt:
- Das erste Element von links, das größer als das Pivot-Element 6 ist, ist die 7.
- Das erste Element von rechts, das kleiner als die 6 ist, ist die 4.
- Wir vertauschen die 7 und die 4.
Die 3 befand sich bereits auf der richtigen Seite (kleiner als 6, also links). Ich habe sie schwächer eingefärbt, da wir sie nicht weiter betrachten müssen.
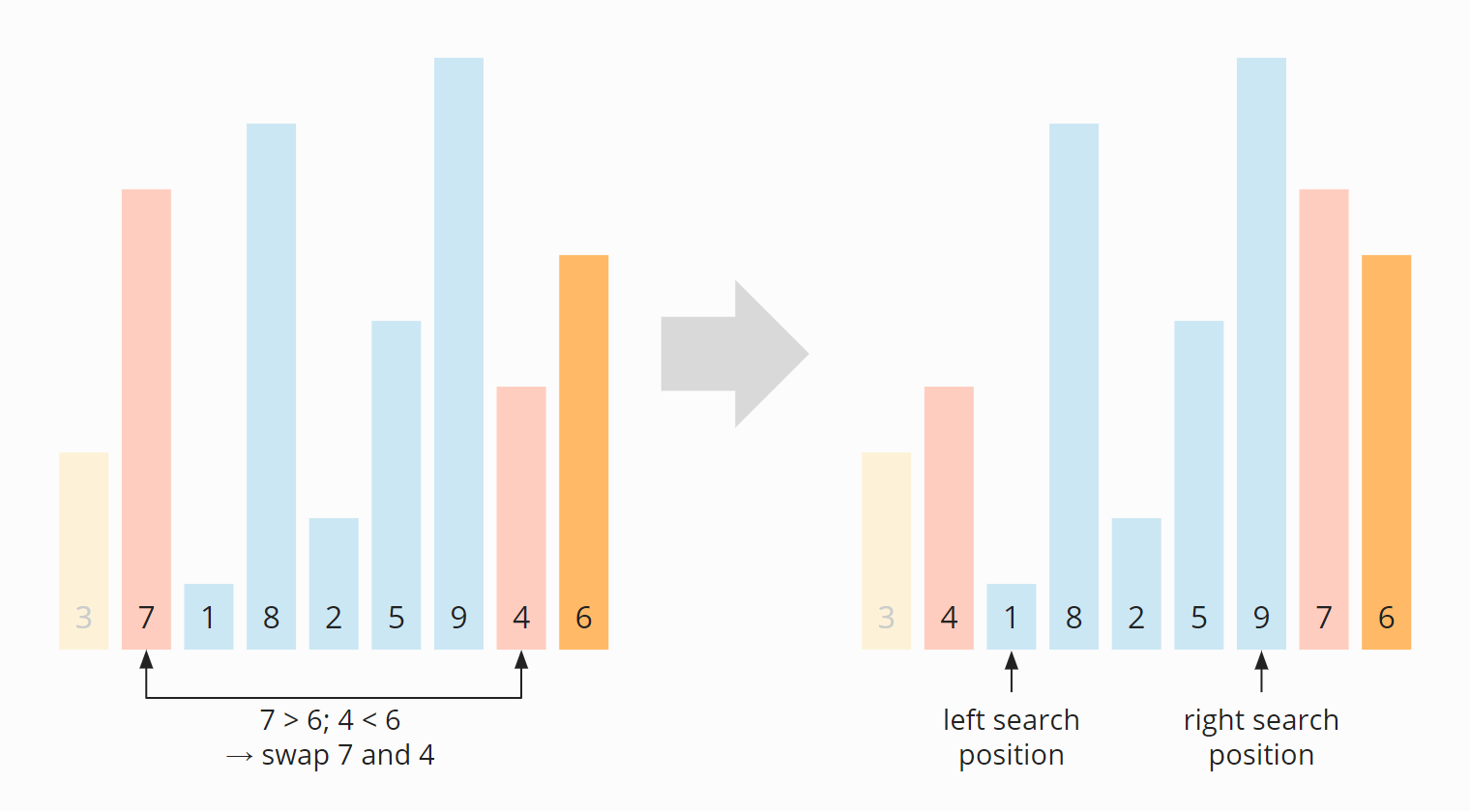
Wir suchen weiter und finden von links aus die 8 (die 1 ist schon auf der richtigen Seite, da kleiner als 6) und von rechts aus die 5 (die 9 ist ebenfalls bereits auf der richtigen Seite, da größer als 6). Wir vertauschen die 8 und die 5:
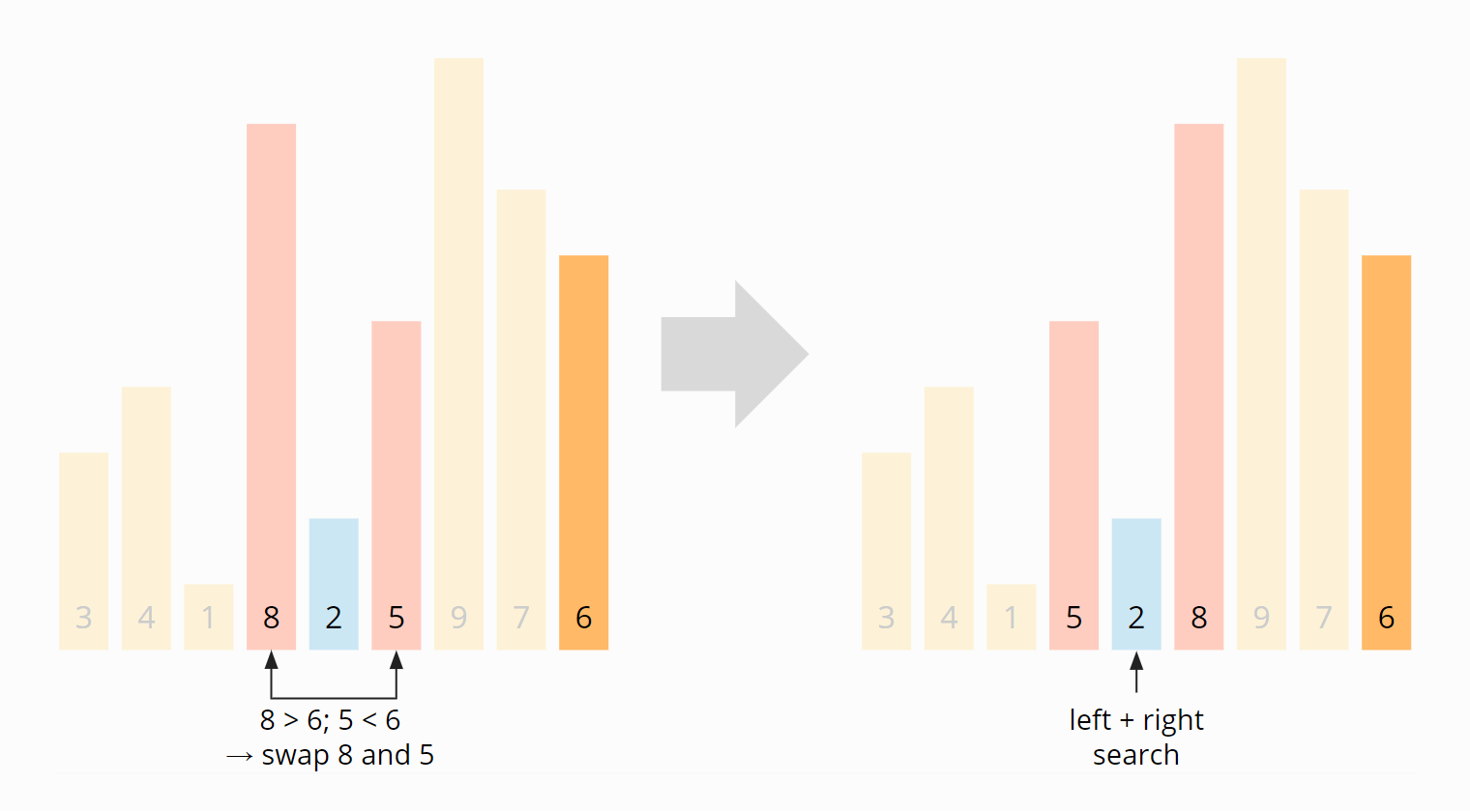
Nun treffen sich die linke und rechte Suchposition an der 2. Das Vertauschen endet hier. Da die 2 kleiner ist als das Pivot-Element, schieben wir den Suchzeiger noch eine Position nach rechts, auf die 8, so dass alle Elemente ab dieser Position größer oder gleich dem Pivot-Element sind und alle Elemente davor kleiner:

Damit das Pivot-Element am Anfang der rechten Partition steht, vertauschen wir noch die 8 mit der 6:
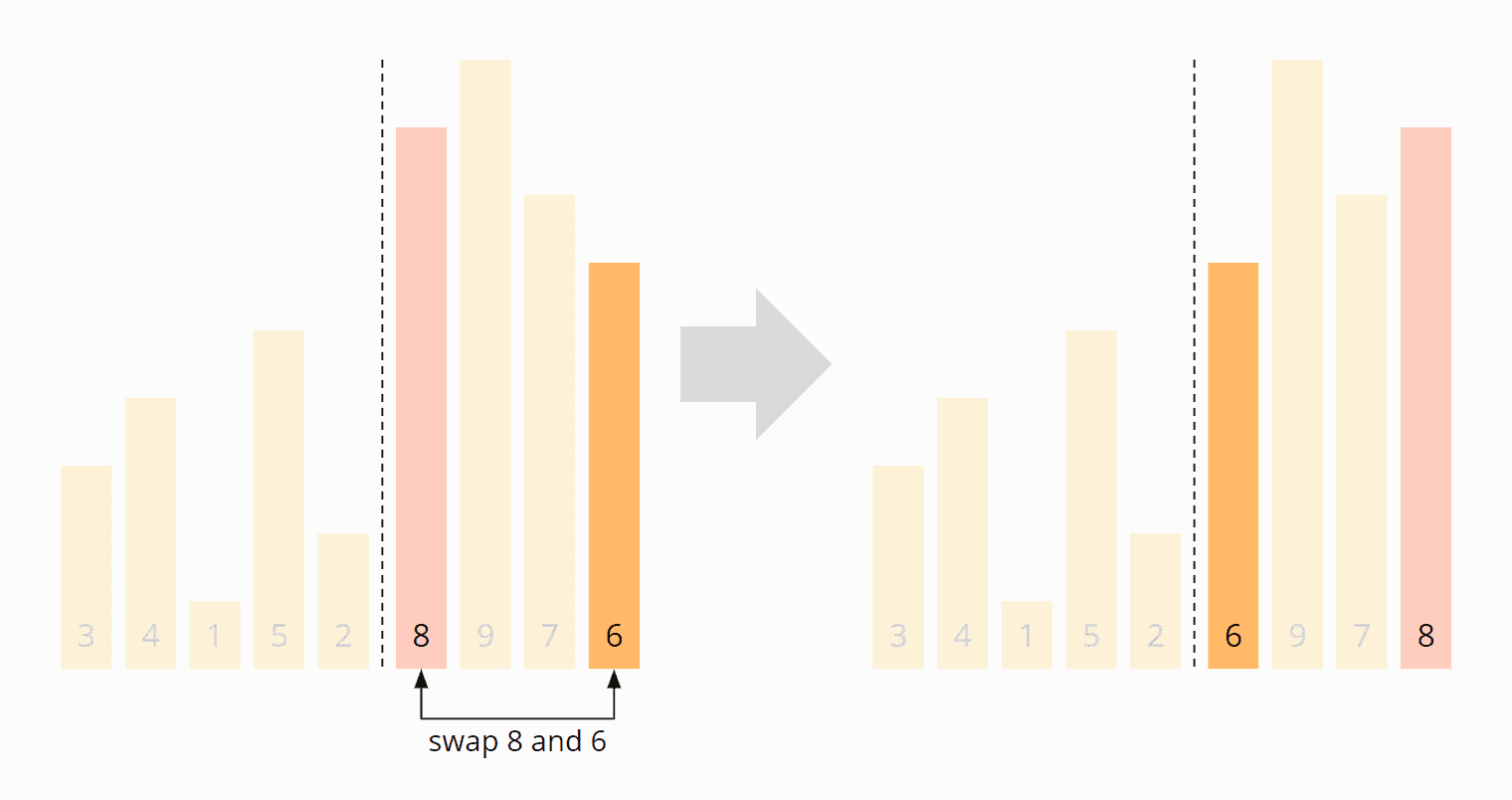
Die Partitionierung ist abgeschlossen: Die 6 befindet sich an der richtigen Position, die Zahlen links von der 6 sind kleiner und die Zahlen rechts davon größer. Wir haben also den Stand erreicht, der im vorangegangenen Abschnitt nach der ersten Partitionierung gezeigt wurde:
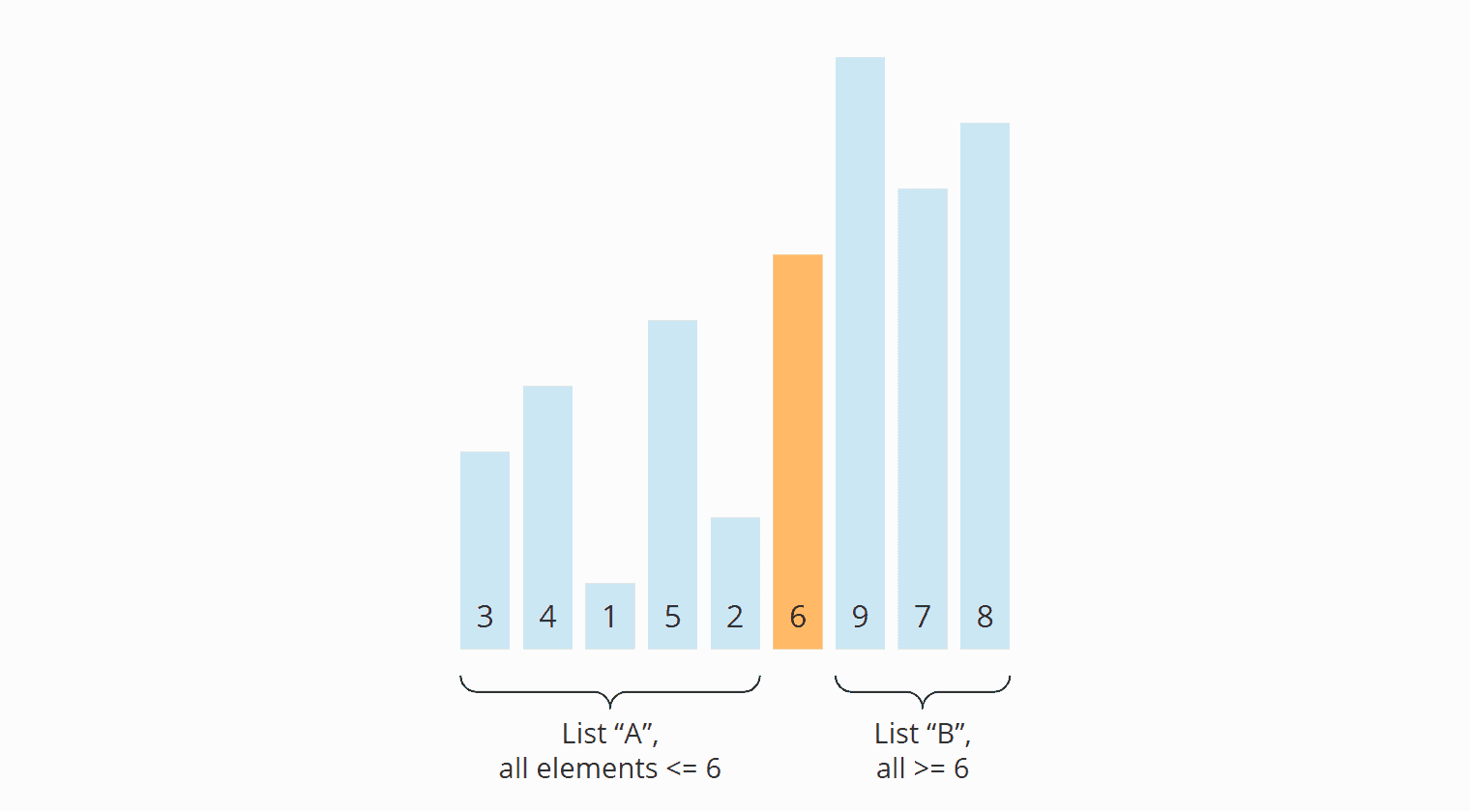
Das Pivot-Element
"Pivot" ist französisch und bedeutet "Dreh- und Angelpunkt".
Im vorangegangenen Beispiel habe ich jeweils das letzte Element eines (Teil-)Arrays als Pivot-Element ausgewählt. Diese Strategie hat den Vorteil, dass sie den Algorithmus besonders einfach macht; sie kann sich aber negativ auf die Performance auswirken.
Vorteil der Pivot-Strategie "letztes Element"
Der Vorteil ist, wie oben erwähnt, ein vereinfachter Algorithmus:
Da das Pivot-Element bei dieser Strategie garantiert im rechten Bereich liegt, brauchen wir es bei den Vergleichs- und Tauschoperationen nicht zu berücksichtigen. Außerdem können wir im letzten Schritt der Partitionierung bedenkenlos das erste Element des rechten Bereichs mit dem Pivot-Element vertauschen, um dieses an seine finale Position zu setzen.
Nachteil der Pivot-Strategie "letztes Element"
In der Praxis führt die Strategie zu Problemen bei vorsortierten Eingabedaten. Bei einem aufsteigend sortierten Array wäre das Pivot-Element in jeder Iteration das größte Element.
Damit würde das Array nicht mehr in zwei möglichst gleich große Partitionen aufgeteilt werden, sondern in eine leere (da kein Element größer ist als das Pivotelement), und eine der Länge n-1 (mit allen Elementen außer dem Pivot-Element).
Dies würde sich negativ auf die Performance auswirken (s. Abschnitt "Quicksort Zeitkomplexität").
Bei absteigend sortierte Eingabedaten wäre das Pivot-Element immer das kleinste Element, so dass die Partitionierung ebenfalls immer eine leere Partition und eine der Größe n-1 erzeugen würde.
Alternative Pivot-Strategien
Alternative Strategien für die Auswahl des Pivot-Elements sind z. B.:
- das mittlere Element,
- ein zufälliges Element,
- der Median aus drei, fünf oder mehr Elementen.
Wählt man auf eine dieser Arten das Pivot-Element aus, erhöht sich die Wahrscheinlichkeit, dass die aus der Partitionierung hervorgehenden Teil-Arrays möglichst gleich groß sind.
Wie sich die Wahl der Pivot-Strategie auf die Performance auswirkt, werde ich im Laufe des Artikels erklären.
Warum nicht der Median?
Im optimalen Fall teilt das Pivot-Element das Array in zwei gleich große Hälften. Warum wählt man dann nicht einfach den Median aller Elemente als Pivot-Element?
Aus folgendem Grund: Um den Median zu bestimmen, müsste man das Array erst einmal sortieren. Wir definieren aber gerade erst den Sortieralgorithmus – wir stehen also vor einem klassischen Henne-Ei-Problem.
Quicksort Java Quellcode
Der folgende Java-Quellcode (Klasse QuicksortSimple im GitHub-Repository) verwendet der Einfachheit halber als Pivot-Element immer das rechte Element eines zu sortierenden (Teil-)Arrays.
Wie oben erläutert, ist dies keine gute Wahl, wenn die Eingabedaten bereits sortiert sein könnten. Diese Variante macht den Code aber zunächst einfacher zu verstehen.
public class QuicksortSimple {
public void sort(int[] elements) {
quicksort(elements, 0, elements.length - 1);
}
private void quicksort(int[] elements, int left, int right) {
// End of recursion reached?
if (left >= right) {
return;
}
int pivotPos = partition(elements, left, right);
quicksort(elements, left, pivotPos - 1);
quicksort(elements, pivotPos + 1, right);
}
public int partition(int[] elements, int left, int right) {
int pivot = elements[right];
int i = left;
int j = right - 1;
while (i < j) {
// Find the first element >= pivot
while (elements[i] < pivot) {
i++;
}
// Find the last element < pivot
while (j > left && elements[j] >= pivot) {
j--;
}
// If the greater element is left of the lesser element, switch them
if (i < j) {
ArrayUtils.swap(elements, i, j);
i++;
j--;
}
}
// i == j means we haven't checked this index yet.
// Move i right if necessary so that i marks the start of the right array.
if (i == j && elements[i] < pivot) {
i++;
}
// Move pivot element to its final position
if (elements[i] != pivot) {
ArrayUtils.swap(elements, i, right);
}
return i;
}
}Code-Sprache: Java (java)Erklärung des Quellcodes:
Die Methode sort() ruft quicksort() auf und übergibt das Array sowie die Start- und Endpositionen.
Die Methode quicksort() ruft zuerst die Methode partition() auf, um das Array zu partitionieren. Daraufhin ruft sie sich selbst rekursiv auf – einmal für das Teil-Array links des Pivot-Elements und einmal für das Teil-Array rechts des Pivot-Elements. Die Rekursion endet, wenn quicksort() für ein Sub-Array der Länge 1 oder 0 aufgerufen wird.
Die Methode partition() partitioniert das Array und gibt die Position des Pivot-Elements zurück. Die Variable i stellt den linken Suchzeiger dar, die Variabe j den rechten Suchzeiger. Die einzelnen Schritte der partition()-Methode sind im Code dokumentiert – sie entsprechen den Schritten des Beispiels aus dem Abschnitt "Quicksort Partitionierung".
Quellcode für alternative Pivot-Strategien
Wollen wir nicht das rechte, sondern ein anderes Element als Pivot-Element verwenden, muss der Algorithmus erweitert werden. Es gibt drei Varianten:
Algorithmus-Variante 1
Die einfachste Variante ist es das gewählte Pivot-Element vorab mit dem rechten Element zu tauschen. In diesem Fall kann der restliche Quellcode unverändert bleiben.
Eine entsprechende Implementierung findest du in der Klasse QuicksortVariant1 im GitHub-Repository. In dieser Variante wird vor jeder Partitionierung die Methode findPivotAndMoveRight() aufgerufen, die entsprechend der gewählten Strategie das Pivot-Element auswählt und mit dem Element ganz rechts vertauscht.
Mögliche Pivot-Strategien sind im Enum PivotStrategy definiert und lauten:
RANDOM: ein zufälliges Element wird ausgewählt.LEFT: das linke Element wird ausgewählt.RIGHT: das rechte Element wird ausgewählt (entspricht letztendlich der oben abgedruckten Variante "QuicksortSimple").MIDDLE: das mittlere Element wird ausgewählt.MEDIAN3: der Median aus drei Elementen des Arrays wird als Pivot-Element ausgewählt.
Algorithmus-Variante 2
In dieser Variante beziehen wir das Pivot-Element in den Tauschvorgang ein und tauschen Elemente, die größer oder gleich dem Pivot-Element sind mit Elementen, die kleiner als das Pivot-Element sind.
Wenn wir das Pivot-Element selbst vertauschen, müssen wir uns diese Positionsänderung merken.
Somit befindet sich das Pivot-Element vor dem letzten Schritt der Partitionierung im rechten Bereich und kann ohne weitere Prüfung mit dem ersten Element des rechten Bereichs getauscht werden.
Den Quellcode dieser Variante findest Du in QuicksortVariant2.
Algorithmus-Variante 3
In dieser Variante belassen wir das Pivot-Element während der Partitionierung zunächst an seinem Platz. Dies erreichen wir, in dem wir nur Elemente, die größer als das Pivot-Element sind mit Elementen tauschen, die kleiner als das Pivot-Element sind.
Im letzten Schritt der Partitionierung müssen wir dann prüfen, ob sich das Pivot-Element im linken oder rechten Bereich befindet. Befindet es sich im linken Bereich, müssen wir es mit dem letzten Element des linken Bereichs tauschen; befindet es sich im rechten Bereich, müssen wir es mit dem ersten Element des rechten Bereichs tauschen.
Den Quellcode dieser Variante findest Du in QuicksortVariant3.
Quicksort Zeitkomplexität
Klicke auf den folgenden Link für eine Einführung in "Zeitkomplexität" und "O-Notation" (mit Beispielen und Diagrammen).
Wir bezeichnen im Folgenden die Anzahl der zu sortierenden Elemente mit n.
Zeitkomplexität im best case
Quicksort erreicht optimale Performance, wenn wir die Arrays und Teil-Arrays immer wieder in zwei gleich große Partitionen aufteilen.
Denn dann brauchen wir bei einer Verdopplung der Anzahl der Elemente n nur eine einzige zusätzliche Stufe von Partitionierungen p. Folgendes Diagramm zeigt, dass bei vier Elementen zwei Partitionierungsstufen benötigt werden und bei acht Elementen nur eine mehr:
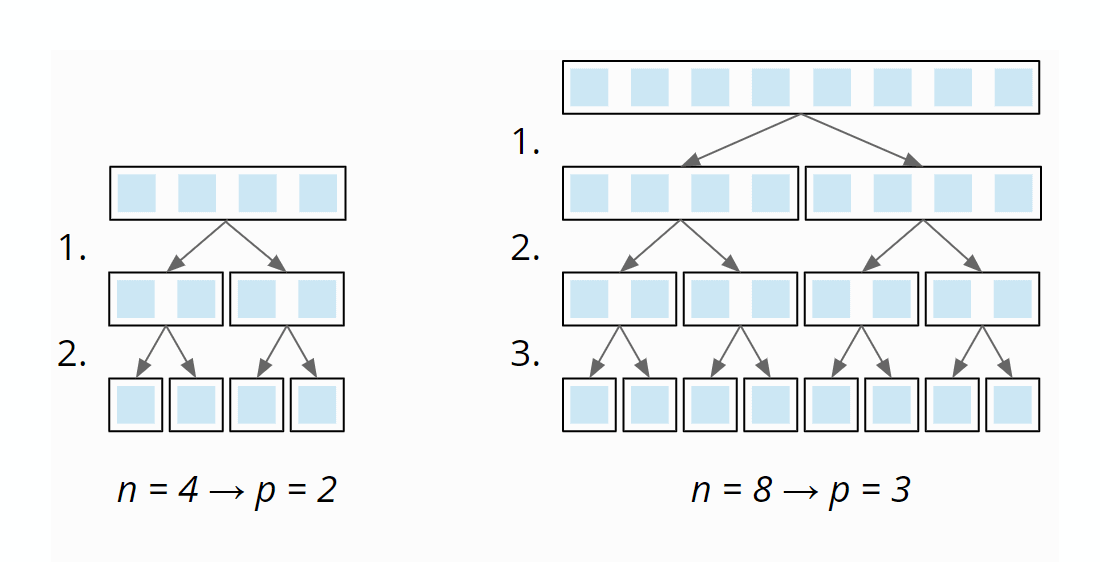
Wir haben also eine Anzahl an Partitionierungsstufen von log2 n.
Auf jeder Partitionierungsstufe müssen wir insgesamt n Elemente auf linke und rechte Partition aufteilen (auf der ersten Ebene 1 × n, auf der zweiten 2 × n/2, auf der dritten 4 × n/4, usw.):
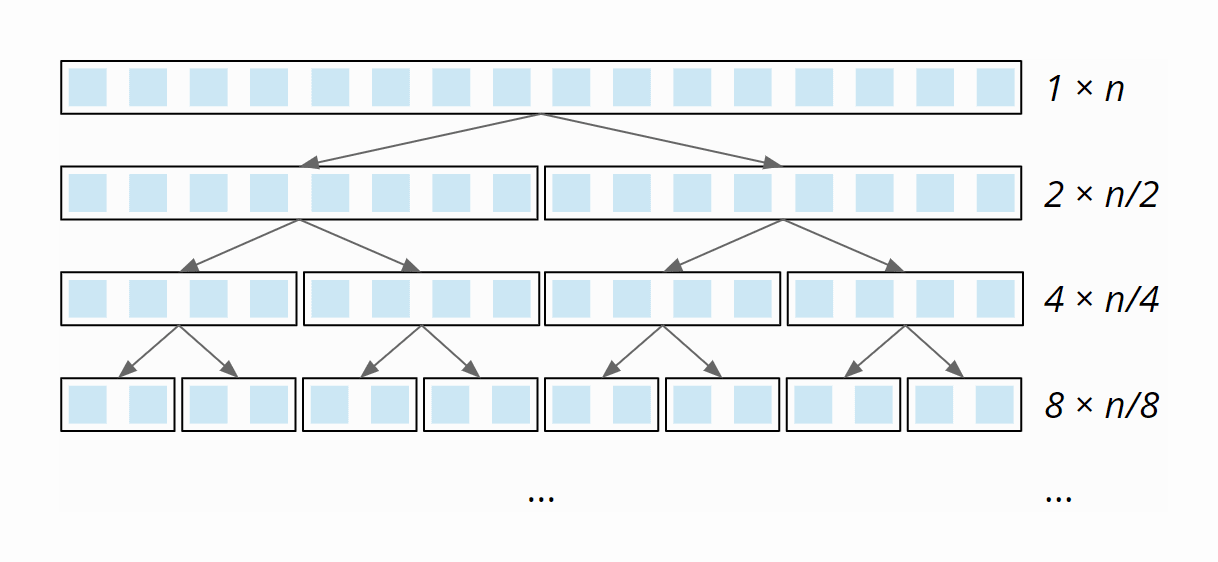
Diese Aufteilung erfolgt – aufgrund der einzelnen Schleife innerhalb der Partitionierung – mit linearem Aufwand: Bei Verdoppelung der Array-Größe verdoppelt sich auch der Partitionierungs-Aufwand. Der Gesamtaufwand ist daher auf allen Partitionierungsstufen gleich.
Wir haben also n Elemente mal log2 n Partitionierungsstufen. Damit gilt:
Die Zeitkomplexität von Quicksort beträgt im best case: O(n log n)
Zeitkomplexität im average case
Die durchschnittliche Zeitkomplexität lässt sich leider nicht ohne komplizierte Mathematik herleiten. Diese würde den Rahmen dieses Artikels sprengen. Ich verwiese hier auf den englischsprachigen Wikipedia-Artikel.
Dieser kommt zu dem Schluss, dass die durchschnittlich Anzahl der Vergleichsoperationen 1,39 n × log2 n beträgt – wir befinden uns also nach wie vor im quasilinearen Aufwand; es gilt:
Die Zeitkomplexität von Quicksort beträgt auch im average case: O(n log n)
Zeitkomplexität im worst case
Wenn das Pivot-Element immer das kleinste oder größte Element des (Teil-)Arrays ist (z. B. weil unsere Eingabedaten bereits sortiert sind und wir als Pivot-Element immer das letzte wählen), würde das Array nicht in zwei etwa gleich große Partitionen aufgeteilt werden, sondern in eine der Länge 0 (da kein Element größer als das Pivot-Element ist) und eine der Länge n-1 (alle Elemente bis auf das Pivot-Element).
Damit bräuchten wir n Partitionierungsstufen mit einem Partitionierungsaufwand der Größe n, n-1, n-2, usw:
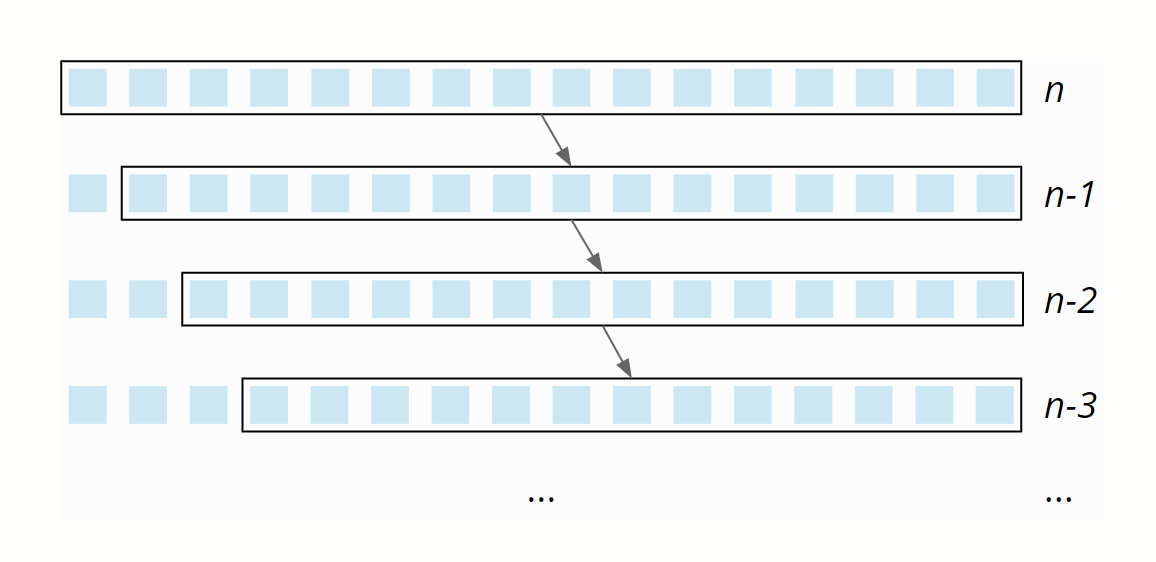
Der Partitionierungsaufwand sinkt linear von n bis 0 – im Mittel beträgt er also ½ n. Bei n Partitionierungsstufen beträgt der Gesamtaufwand also n × ½ n = ½ n². Es gilt somit:
Die Zeitkomplexität von Quicksort beträgt im worst case: O(n²)
In der Praxis würde der Versuch ein aufsteigend oder absteigend vorsortiertes Array mit der Pivot-Strategie "rechtes Element" zu sortieren sehr schnell an einer StackOverflowException scheitern, da die Rekursion so tief gehen müsste wie das Array groß ist.
Java Quicksort Laufzeit
Nach so viel Theorie zurück zur Praxis!
Mit dem Programm UltimateTest können wir die tatsächliche Performance von Quicksort (und allen anderen Algorithmen dieser Artikelserie) messen. Das Programm geht dabei wie folgt vor:
- Es sortiert Arrays der Größe 1.024, 2.048, 4.096, usw. bis maximal 536.870.912 (= 229), bricht dabei allerdings ab, wenn ein einzelner Sortiervorgang 20 Sekunden oder länger benötigt.
- Es wendet den Sortieralgorithmus auf unsortierte Eingabedaten, aufsteigend sortierte und absteigend sortierte Eingabedaten an.
- Es durchläuft zunächst zwei Warmup-Phasen, um dem HotSpot-Compiler ausreichend Zeit zu geben, den Code zu optimieren.
- Das ganze wird so oft wiederholt, bis der Prozess beendet wird.
Laufzeit-Messung der Quicksort-Algorithmus-Varianten
Zunächst müssen wir entscheiden, welche Algorithmus-Variante wir ins Rennen schicken wollen, um den Test nicht ausufern zu lassen. Dafür kombiniert das Programm CompareQuicksorts alle Varianten mit allen Pivot-Strategien und sortiert mit jeder Kombination 50 mal etwa 5,5 Millionen Elemente.
Hier ist das Ergebnis, sortiert nach Laufzeit (Datei Quicksort_Pivot_Strategies.log):
| Variante | Pivot-Strategie | Median |
|---|---|---|
| QuicksortSimple | RIGHT | 458,5 ms |
| QuicksortVariant1 | RIGHT | 460,4 ms |
| QuicksortVariant1 | MIDDLE | 461,7 ms |
| QuicksortVariant3 | RIGHT | 472,4 ms |
| QuicksortVariant3 | MIDDLE | 473,5 ms |
| QuicksortVariant2 | RIGHT | 477,9 ms |
| QuicksortVariant2 | MIDDLE | 483,4 ms |
| QuicksortVariant1 | MEDIAN3 | 489,8 ms |
| QuicksortVariant3 | MEDIAN3 | 507,4 ms |
| QuicksortVariant2 | MEDIAN3 | 508,6 ms |
| QuicksortVariant1 | RANDOM | 516,1 ms |
| QuicksortVariant3 | RANDOM | 528,9 ms |
| QuicksortVariant2 | RANDOM | 534,2 ms |
Folgendes lässt sich ablesen:
- Der simple Algorithmus ist am schnellsten.
- Für alle Algorithmus-Varianten ist die Pivot-Strategie RIGHT am schnellsten, dicht gefolgt von MIDDLE, danach mit etwas größerem Abstand MEDIAN3 (der Overhead ist hier offenbar größer als der Gewinn), und am langsamsten ist RANDOM (Zufallszahlen zu generieren ist teuer).
- Für alle Pivot-Strategien ist Variante 1 am schnellsten, Variante 3 am zweitschnellsten und Variante 2 am langsamsten.
Laufzeit-Messungen für verschiedene Pivot-Strategien und Array-Größen
Aufgrund dieses Ergebnisses führe ich den UltimateTest mit Algorithmus-Variante 1 aus (Pivot-Element wird vorab mit dem rechten Element vertauscht).
In den folgenden Abschnitten findest du die Ergebnisse für die verschiedenen Pivot-Strategien nach 50 Iterationen (dies sind nur Auszüge; das vollständige Testergebnis findest du in UltimateTest_Quicksort.log).
Messergebnisse für Pivot-Strategie "rechtes Element"
| n | unsortiert | aufsteigend | absteigend |
|---|---|---|---|
| 1.024 | 0,051 ms | 0,155 ms | 0,158 ms |
| 2.048 | 0,100 ms | 0,578 ms | 0,597 ms |
| 4.096 | 0,208 ms | 2,247 ms | 2,322 ms |
| 8.192 | 0,436 ms | 8,906 ms | 9,127 ms |
| 16.384 | 0,920 ms | StackOverflow | StackOverflow |
| 32.768 | 1,941 ms | StackOverflow | StackOverflow |
| ... | ... | ... | ... |
| 33.554.432 | 3.099,994 ms | StackOverflow | StackOverflow |
| 67.108.864 | 6.421,172 ms | StackOverflow | StackOverflow |
| 134.217.728 | 13.305,377 ms | StackOverflow | StackOverflow |
| 268.435.456 | 27.493,636 ms | StackOverflow | StackOverflow |
Folgendes lässt sich ablesen:
- Bei zufällig verteilten Eingabedaten verlängert sich die benötigte Zeit um etwas mehr als das doppelte, wenn sich die Größe des zu sortierenden Arrays verdoppelt. Dies entspricht der erwarteten quasi-linearen Laufzeit – O(n log n).
- Bei aufsteigend oder absteigend sortierten Eingabedaten vervierfacht sich die benötigte Zeit bei verdoppelter Eingabegröße, hier haben wir also quadratische Zeit – O(n²).
- Absteigend sortierte Daten zu sortieren dauert nur wenig länger als aufsteigend sortierte Daten zu sortieren.
- Bei nur 8.192 Elementen wird für das Sortieren vorsortierter Eingabedaten bereits 23 mal so lange benötigt wie für das Sortieren unsortierter Daten.
- Bei mehr als 8.192 Elementen kommt es bei vorsortierten Eingabedaten zur gefürchteten
StackOverflowException.
Messergebnisse für Pivot-Strategie "mittleres Element"
| n | unsortiert | aufsteigend | absteigend |
|---|---|---|---|
| ... | ... | ... | ... |
| 16.777.216 | 1.508 ms | 191,3 ms | 227,0 ms |
| 33.554.432 | 3.127 ms | 409,5 ms | 464,7 ms |
| 67.108.864 | 6.486 ms | 806,4 ms | 942,9 ms |
| 134.217.728 | 13.409 ms | 1.727,2 ms | 1.945,8 ms |
| 268.435.456 | 27.740 ms | 3.405,2 ms | 3.959,2 ms |
Es lässt sich ablesen:
- Sowohl für unsortierte als auch sortierte Eingabedaten wird bei Verdoppelung der Array-Größe etwas mehr als die doppelte Zeit benötigt. Dies entspricht der erwarteten quasi-linearen Laufzeit – O(n log n).
- Für bereits sortierte Eingabedaten ist der Algorithmus deutlich schneller als für zufällig angeordnete – und zwar sowohl für aufsteigend als auch für absteigend sortierte Daten.
- Die Performance-Verlust durch den Vorabtausch des mittleren mit dem rechten Element beträgt in allen Tests mit unsortierten Eingabedaten weniger als 0,9 %.
Messergebnisse für Pivot-Strategie "Median aus drei Elementen"
| n | unsortiert | aufsteigend | absteigend |
|---|---|---|---|
| ... | ... | ... | ... |
| 16.777.216 | 1.589 ms | 222,6 ms | 249,0 ms |
| 33.554.432 | 3.291 ms | 473,2 ms | 514,4 ms |
| 67.108.864 | 6.807 ms | 934,6 ms | 1.039,1 ms |
| 134.217.728 | 14.066 ms | 1.980,5 ms | 2.142,8 ms |
| 268.435.456 | 29.041 ms | 3.907,6 ms | 4.349,2 ms |
Es lässt sich ablesen:
- Auch hier haben wir in allen Fällen quasi-linearen Aufwand – O(n log n).
- Wie schon beim Vergleich der Algorithmus-Varianten ist die Pivot-Strategie "Median aus drei Elementen" etwas langsamer als die Strategie "mittleres Element".
Überblick über alle Messergebnisse
Hier findest du die Messergebnisse noch einmal als Diagramm (absteigend sortierte Eingabedaten habe ich der Übersicht halber weggelassen):

Man sieht noch einmal schön, dass die Strategie "Rechtes Element" für aufsteigend sortierte Daten zu quadratischem Aufwand führt (rote Linie) und für unsortierte Daten am schnellsten ist (blaue Linie). Am zweitschnellsten (mit minimalem Abstand) ist die Pivot-Stragie "Mittleres Element" (gelbe Linie).
Quicksort optimiert: Kombination mit Insertion Sort
Für sehr kleine Arrays ist Insertion Sort schneller als Quicksort, daher werden in der Praxis diese Algorithmen häufig kombiniert. D. h. (Sub-)Arrays werden ab einer bestimmten Größe nicht weiter partitioniert, sondern mit Insertion Sort sortiert.
Quicksort/Insertion Sort Quellcode
Die Quellcode-Änderungen gegenüber des Standard-Quicksorts sind sehr überschaubar und beschränken sich auf die quicksort()-Methode. Hier noch einmal die Methode aus dem Standard-Algorithmus:
private void quicksort(int[] elements, int left, int right) {
// End of recursion reached?
if (left >= right) {
return;
}
int pivotPos = partition(elements, left, right);
quicksort(elements, left, pivotPos - 1);
quicksort(elements, pivotPos + 1, right);
}Code-Sprache: Java (java)Und hier die optimierte Variante, wobei die Variablen insertionSort und partitioningAlgorithm Instanzen des Insertion-Sort- und des Quicksort-Algorithmus sind. Hinzugekommen ist hier lediglich der mit "Threshold for insertion sort reached?" kommentierte Code-Block in der Mitte der Methode:
private void quicksort(int[] elements, int left, int right) {
// End of recursion reached?
if (left >= right) {
return;
}
// Threshold for insertion sort reached?
if (right - left < threshold) {
insertionSort.sort(elements, left, right + 1);
return;
}
int pivotPos = partitioningAlgorithm.partition(elements, left, right);
quicksort(elements, left, pivotPos - 1);
quicksort(elements, pivotPos + 1, right);
}Code-Sprache: Java (java)Den kompletten Quellcode findest du in der Klasse QuicksortImproved im GitHub-Repository. Als Konstruktorparameter wird der Grenzwert für das Umschalten auf Insertion Sort, threshold, übergeben, sowie eine Instanz der zu verwendenden Quicksort-Variante.
Quicksort/Insertion Sort Performance
Das Programm CompareImprovedQuickSort misst die benötigte Zeit zum Sortieren von etwa 5,5 Millionen Elementen bei verschiedenen Grenzwerten für das Umschalten auf Insertion Sort.
Da das optimierte Quicksort nur Arrays ab einer gewissen Größe partitioniert, könnte der Einfluss der Pivot-Strategie und der Algorithmus-Variante eine andere Rolle spielen als bisher. Um dies zu berücksichtigen, testet das Programm die Grenzwerte für alle drei Algorithmus-Varianten sowie die Pivot-Strategien "Mitte" und "Median aus drei Elementen".
Die kompletten Messergebnisse findest du in CompareImprovedQuicksort.log.
Wie auch in den vorangegangenen Tests performen hier Algorithmus-Variante 1 und Pivot-Strategie "Mittleres Element" durchgehend am besten.
Hier die Messwerte für die gewählte Kombination und verschiedene Grenzwerte für das Umschalten auf Insertion Sort:
| Grenzwert | Laufzeit |
|---|---|
| 0 (= reguläres Quicksort) | 492,6 ms |
| 2 | 492,6 ms |
| 4 | 476,1 ms |
| 8 | 456,1 ms |
| 16 | 436,0 ms |
| 24 | 427,2 ms |
| 32 | 423,1 ms |
| 48 | 422,3 ms |
| 64 | 425,3 ms |
| 96 | 438,0 ms |
| 128 | 454,9 ms |
| 196 | 493,4 ms |
Hier die Messwerte in grafischer Darstellung:

Resultat:
Durch das Umschalten auf Insertion Sort für (Sub-)Arrays, die 48 oder weniger Elemente enthalten, können wir die Laufzeit von Quicksort bei 5,5 Millionen Elementen auf etwa 85 % des ursprünglichen Wertes reduzieren.
Wie sich der optimierte Quicksort-Algorithmus bei anderen Eingabegrößen schlägt, erfährst du im Abschnitt "Vergleich aller Quicksort-Optimierungen".
Dual-Pivot Quicksort
Quicksort lässt sich noch weiter optimieren, in dem man nicht ein Pivot-Element verwendet, sondern zwei. Bei der Partitionierung werden die Elemente dann aufgeteilt in:
- Elemente kleiner als das kleinere Pivot-Element,
- Elemente größer als/gleich wie das kleinere Pivot-Element und kleiner als das größere Pivot-Element,
- Elemente größer als/gleich wie das größere Pivot-Element.
Auch hier gibt es unterschiedliche Pivot-Strategien, z. B.:
- Linkes und rechtes Element: Dies führt – analog zum regulären Quicksort – dazu, dass bei sortierten Elementen zwei Partitionen leer bleiben und eine Partition n-2 Elemente enthält. Dies wiederum resultiert in quadratischem Aufwand und
StackOverflowExceptionsschon bei vergleichsweise kleinen n. - Elemente an den Position "ein Drittel" und "zwei Drittel": Dies ist vergleichbar mit der Strategie "Mittleres Element" im regulären Quicksort.
Das folgende Diagramm zeigt eine beispielhafte Partitionierung mit zwei Pivot-Elementen an den "Drittel"-Positionen:
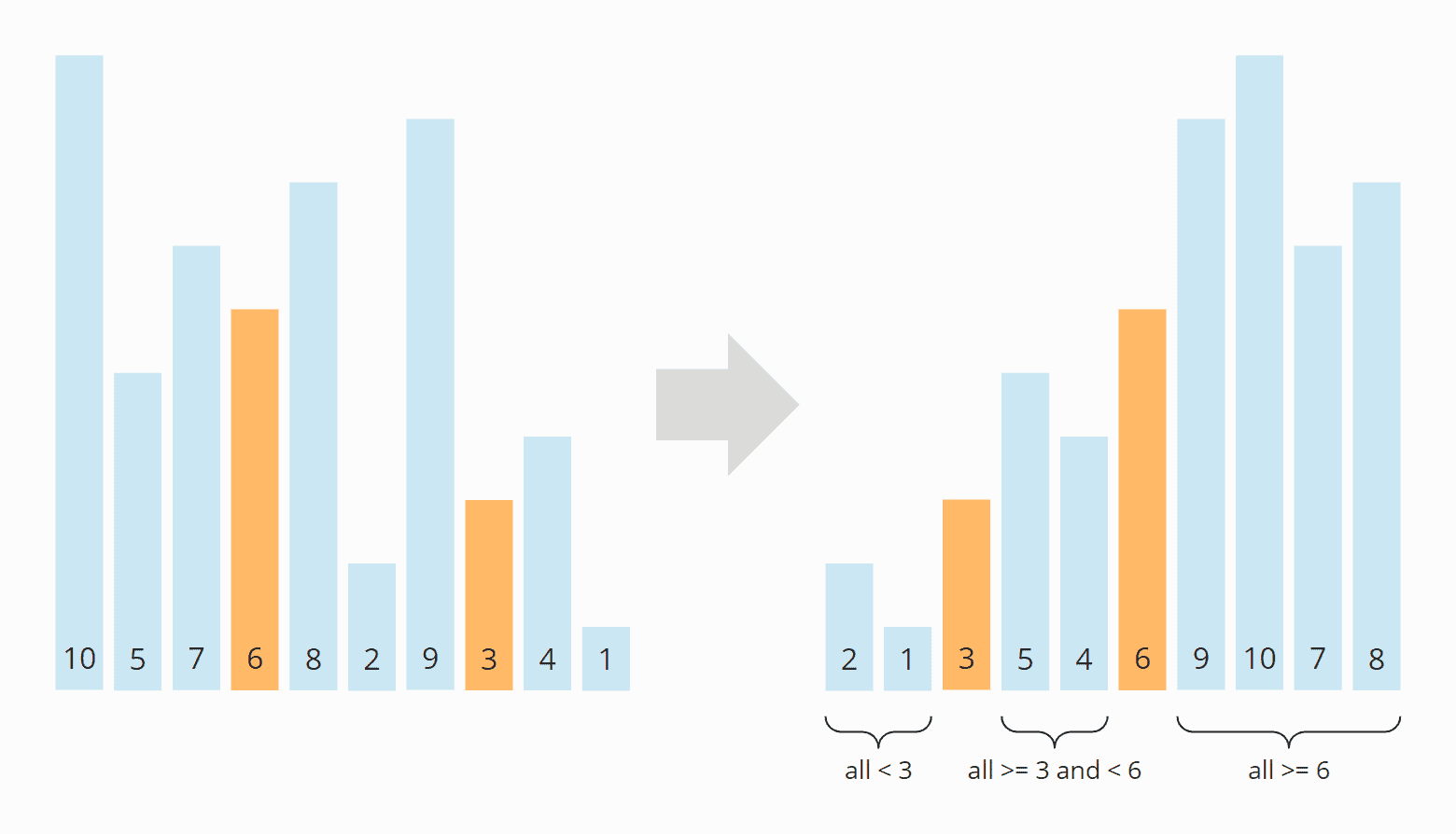
Dual-Pivot Quicksort wird (mit zusätzlichen Optimierungen) im JDK von der Methode Arrays.sort() eingesetzt.
Dual-Pivot Quicksort Quellcode
Die quicksort()-Methode ruft sich – im Vergleich zum regulären Algorithmus – nicht für zwei, sondern für drei Partitionen rekursiv auf:
private void quicksort(int[] elements, int left, int right) {
// End of recursion reached?
if (left >= right) {
return;
}
int[] pivotPos = partition(elements, left, right);
int p0 = pivotPos[0];
int p1 = pivotPos[1];
quicksort(elements, left, p0 - 1);
quicksort(elements, p0 + 1, p1 - 1);
quicksort(elements, p1 + 1, right);
}Code-Sprache: Java (java)Die partition()-Methode ruft zunächst findPivotsAndMoveToLeftRight() auf, welche anhand der gewählten Pivot-Strategie die Pivot-Elemente auswählt und mit den Elementen links und rechts vertauscht (analog zum Vertauschen des Pivot-Elements mit dem rechten Elemente im regulären Quicksort).
Danach laufen wieder zwei Suchzeiger von links und rechts über das Array und vergleichen und tauschen die Elemente, so dass diese am Ende auf drei Partitionen aufgeteilt sind. Wie genau sie das tun, lässt sich anhand der sprechenden Variablennamen einigermaßen gut am Quellcode ablesen.
int[] partition(int[] elements, int left, int right) {
findPivotsAndMoveToLeftRight(elements, left, right);
int leftPivot = elements[left];
int rightPivot = elements[right];
int leftPartitionEnd = left + 1;
int leftIndex = left + 1;
int rightIndex = right - 1;
while (leftIndex <= rightIndex) {
// elements < left pivot element?
if (elements[leftIndex] < leftPivot) {
ArrayUtils.swap(elements, leftIndex, leftPartitionEnd);
leftPartitionEnd++;
}
// elements >= right pivot element?
else if (elements[leftIndex] >= rightPivot) {
while (elements[rightIndex] > rightPivot && leftIndex < rightIndex) {
rightIndex--;
}
ArrayUtils.swap(elements, leftIndex, rightIndex);
rightIndex--;
if (elements[leftIndex] < leftPivot) {
ArrayUtils.swap(elements, leftIndex, leftPartitionEnd);
leftPartitionEnd++;
}
}
leftIndex++;
}
leftPartitionEnd--;
rightIndex++;
// move pivots to their final positions
ArrayUtils.swap(elements, left, leftPartitionEnd);
ArrayUtils.swap(elements, right, rightIndex);
return new int[]{leftPartitionEnd, rightIndex};
}Code-Sprache: Java (java)Die Methode findPivotsAndMoveToLeftRight() arbeitet wie folgt:
Bei der Pivot-Strategie LEFT_RIGHT prüft sie, ob das ganz linke Element kleiner ist als das ganz rechte. Wenn nicht, werden beide vertauscht.
Bei der Strategie THIRDS werden zunächst die Elemente an den Positionen "ein Drittel" (Variable first) und "zwei Drittel" (Variable second) extrahiert. Danach folgt eine Reihe von if-Abfragen, die letztendlich bloß das größere der beiden Elemente nach ganz rechts setzt und das kleinere der beiden Elemente nach ganz links.
(Der Code wird dadurch so aufgebläht, dass zwei Sonderfälle berücksichtigt werden müssen: In sehr kleinen Partitionen könnte das erste Pivotelement auf das ganz linke Element fallen und das zweite Pivotelement auf das ganz rechte Element.)
private void findPivotsAndMoveToLeftRight(int[] elements,
int left, int right) {
switch (pivotStrategy) {
case LEFT_RIGHT -> {
if (elements[left] > elements[right]) {
ArrayUtils.swap(elements, left, right);
}
}
case THIRDS -> {
int len = right - left + 1;
int firstPos = left + (len - 1) / 3;
int secondPos = right - (len - 2) / 3;
int first = elements[firstPos];
int second = elements[secondPos];
if (first > second) {
if (secondPos == right) {
if (firstPos == left) {
ArrayUtils.swap(elements, left, right);
} else {
// 3-way swap
elements[right] = first;
elements[firstPos] = elements[left];
elements[left] = second;
}
} else if (firstPos == left) {
// 3-way swap
elements[left] = second;
elements[secondPos] = elements[right];
elements[right] = first;
} else {
ArrayUtils.swap(elements, firstPos, right);
ArrayUtils.swap(elements, secondPos, left);
}
} else {
if (secondPos != right) {
ArrayUtils.swap(elements, secondPos, right);
}
if (firstPos != left) {
ArrayUtils.swap(elements, firstPos, left);
}
}
}
default -> throw new IllegalStateException("Unexpected value: " + pivotStrategy);
}
}Code-Sprache: Java (java)Den vollständigen Quellcode findest Du in der Datei DualPivotQuicksort.
Dual-Pivot Quicksort Performance
Ob und inwieweit Dual-Pivot Quicksort die Performance verbessert, findest du im Abschnitt "Vergleich aller Quicksort-Optimierungen" heraus.
Dual-Pivot Quicksort kombiniert mit Insertion Sort
Genau wie das reguläre Quicksort kann auch Dual-Pivot Quicksort mit Insertion Sort kombiniert werden. Die Quellcode-Änderungen entsprechen denen für das reguläre Quicksort (s. Abschnitt "Quicksort/Insertion Sort Quellcode"). Ich gehe daher hier nicht noch einmal im Detail darauf ein.
Den Quellcode findest du in DualPivotQuicksortImproved.
Das Programm CompareImprovedDualPivotQuicksort testet den Algorithmus für verschiedene Grenzwerte für das Umschalten auf Insertion Sort.
Die Messwerte findest du in CompareImprovedDualPivotQuicksort.log. Hier sind sie als Diagramm:
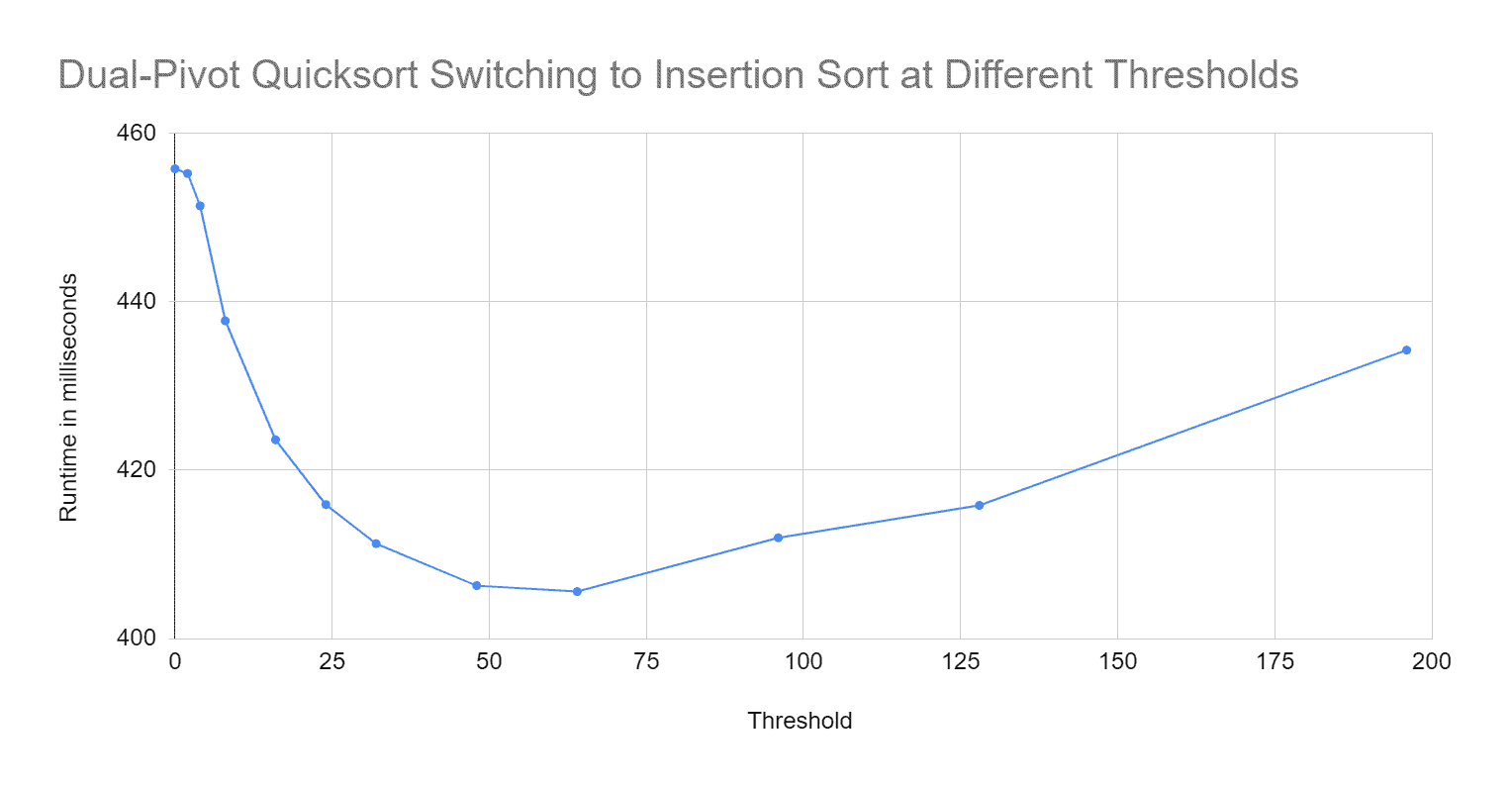
Es lohnt sich also bei Dual-Pivot-Quicksort (Sub-)Arrays mit 64 Elementen oder weniger mit Insertion Sort zu sortieren.
Vergleich aller Quicksort-Optimierungen
Mit dem in Abschnitt "Java Quicksort Laufzeit" erwähnten UltimateTest vergleiche ich abschließend noch einmal die Performance folgender Algorithmen:
- Reguläres Quicksort mit Pivot-Strategie "Mittleres Element",
- Quicksort kombiniert mit Insertion Sort und einem Schwellwert von 48,
- Dual-Pivot Quicksort mit Pivot-Strategie "Elemente an den Positionen ein Drittel und zwei Drittel",
- Dual-Pivot Quicksort kombiniert mit Insertion Sort und einem Schwellwert von 64,
Arrays.sort()des JDK (die JDK-Entwickler haben ihren Dual-Pivot Quicksort-Algorithmus so weit optimiert, dass es sich bei diesem schon bei 44 Elementen lohnt auf Insertion Sort umzuschalten).
Das Ergebnis findest Du in UltimateTest_Quicksort_Optimized.log – und in folgendem Diagramm:

Zunächst einmal ist sehr schön der quasi-lineare Aufwand aller Varianten zu erkennen.
Die Performance von Dual-Pivot-Quicksort ist sichtbar besser als die des regulären Quicksort – bei einer Viertelmilliarde Elemente etwa 5 %. Die Kombinationen mit Insertion Sort bringen jeweils mindestens 10 % Performancegewinn.
An die Sortiermethode des JDK kommen die Eigenimplementierungen nicht ganz heran – es fehlen noch etwa 6 %. Die JDK-Methode wurde im Laufe der Jahre hoch optimiert. Wenn dich interessiert, wie genau, dann kannst du dir den Quellcode auf GitHub anschauen.
Außerdem ist gut zu erkennen, dass alle Varianten vorsortierte Daten deutlich schneller sortieren als unsortierte – und aufsteigend sortierte Daten etwas schneller als absteigend sortierte. Arrays.sort() ist auch für vorsortierte Daten optimiert, so dass die entsprechende Linie nur minimal über der Null-Linie liegt (172,7 ms bei einer Viertelmilliarde Elemente).
Weitere Eigenschaften von Quicksort
Als weitere Eigenschaften werden in diesem Kapitel die Platzkomplexität von Quicksort betrachtet, die Stabilität sowie die Parallelisierbarkeit.
Platzkomplexität von Quicksort
Für jede Rekursionsstufe brauchen wir zusätzlichen Speicher auf dem Stack. Im average und best case ist die maximale Rekursionstiefe durch O(log n) begrenzt (s. Abschnitt "Zeitkomplexität").
Im worst case ist die maximale Rekursionstiefe n.
Der Algorithmus kann allerdings durch Endrekursion insoweit optimiert werden, dass immer nur die kleinere Partition durch Rekursion weiterverarbeitet wird und die größere durch Iteration.
Da die kleinere Teilpartition maximal halb so groß ist wie die Ausgangspartition (andernfalls wäre sie nicht die kleinere, sondern die größere Teilpartition), kommt es mit Endrekursion auch im worst case maximal zu einer Rekursionstiefe von log2 n.
Der zusätzliche Speicherbedarf pro Rekursionsstufe ist konstant. Somit gilt:
Die Platzkomplexität von Quicksort ist im best und average case und – bei Einsatz von Endrekursion auch im worst case – O(log n)
Stabilität von Quicksort
Durch die Art und Weise, wie Elemente innerhalb der Partitionierung auf die Teilbereiche aufgeteilt werden, können Elemente mit gleichem Key ihre ursprüngliche Reihenfolge ändern.
Hier ein simples Beispiel: Partitioniert werden soll das Array [7, 8, 7, 2, 6] mit der Pivot-Strategie "Rechtes Element". (Die zweite 7 habe ich als 7' gekennzeichnet, um sie von der ersten unterscheiden zu können.)
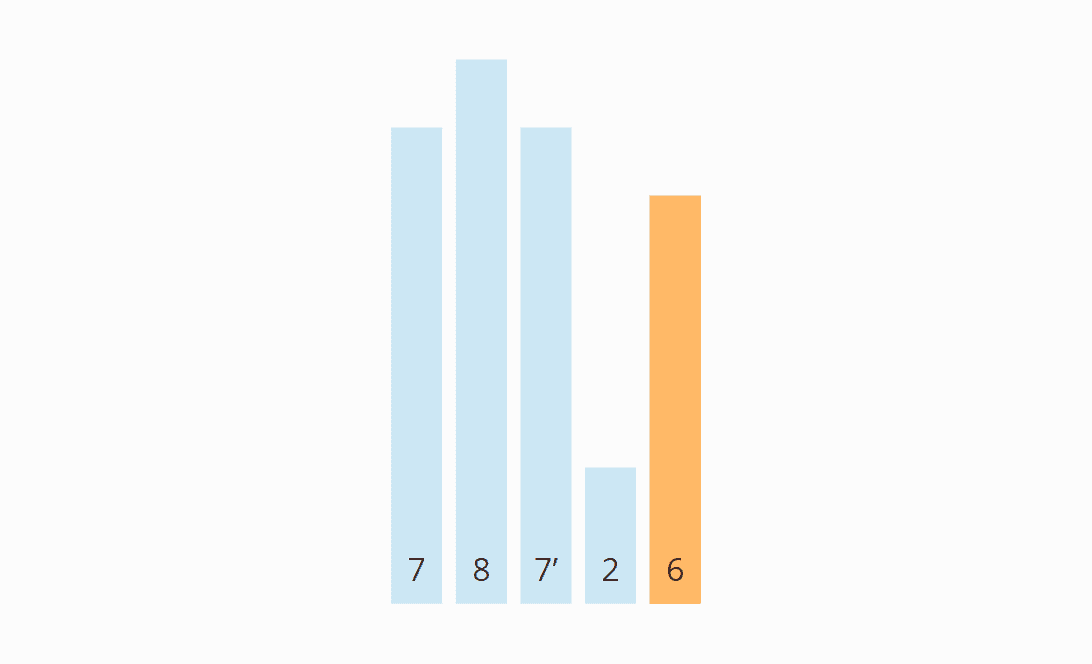
Das erste Element von links, das größer als die 6 ist, ist die erste 7. Das erste Element von rechts, das kleiner als die 6 ist, ist die 2. Es müssen also die erste 7 und die 2 vertauscht werden:

Die erste 7 befindet sich danach nicht mehr vor, sondern hinter der zweiten 7 (7'). Dies bleibt auch so, nachdem das erste Element der rechten Partition (die 8) mit dem Pivot-Element (der 6) vertauscht wurde:
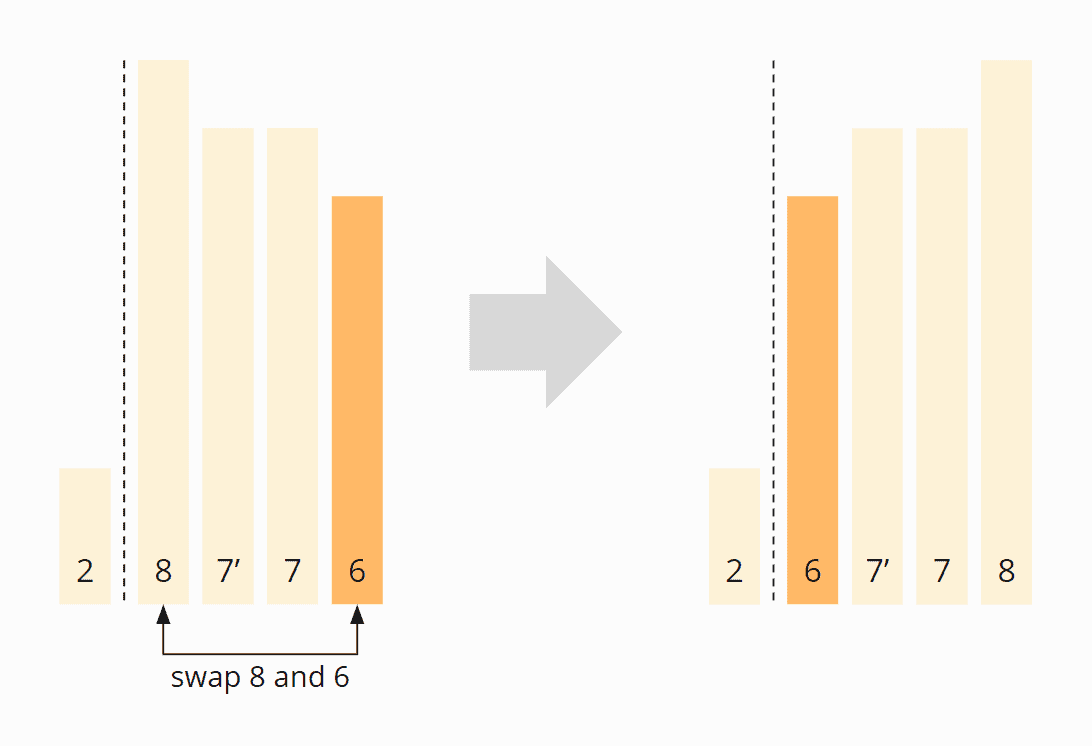
Quicksort ist demzufolge nicht stabil.
Parallelisierbarkeit von Quicksort
Es gibt verschiedene Varianten Quicksort zu parallelisieren.
Zum einen lassen sich mehrere Partitionen parallel weiter partitionieren. Bei dieser Variante kann jedoch die erste Partitionierungsstufe gar nicht parallelisiert werden, in der zweiten Stufe können nur zwei Cores ausgelastet werden, in der dritten nur vier, usw.
Es gibt mehrere andere, ausgefeiltere Varianten; eine Zusammenfassung findest du in diesem englischsprachigen Artikel über paralleles Quicksort.
Quicksort vs. Mergesort
Einen Vergleich der Laufzeiten von Quicksort und Mergesort findest du im Artikel über Mergesort.
Zusamenfassung
Quicksort ist ein effizienter, instabiler Sortieralgorithmus mit einer Zeitkomplexität von O(n log n) im best und average case und O(n²) im worst case.
Für sehr kleine n ist Quicksort langsamer als Insertion Sort und wird daher in der Praxis in der Regel mit Insertion Sort kombiniert.
Die Methode Arrays.sort() im JDK verwendet eine Dual-Pivot Quicksort-Implementierung, die (Teil-)Arrays mit weniger als 44 Elementen mit Insertion Sort sortiert.
Weitere Sortieralgorithmen findest du in der Übersicht aller Sortieralgorithmen und ihrer Eigenschaften im ersten Teil der Artikelserie.
