

Dieser Artikel ist Teil der Serie "Sortieralgorithmen: Ultimate Guide" und...
- beschreibt die Funktionsweise von Insertion Sort,
- zeigt eine Implementierung in Java,
- leitet die Zeitkomplexität her
- und überprüft, ob die Performance der Java-Implementierung mit dem erwarteten Laufzeitverhalten übereinstimmt.
Die Quellcodes der gesamten Artikelserie findest du in meinem GitHub-Repository.
Beispiel: Sortieren von Spielkarten
Beginnen wir mit einem Spielkartenbeispiel.
Stell dir vor, du bekommst eine Karte nach der anderen gereicht. Du nimmst die erste Karte auf die Hand. Die zweite sortierst du dann links oder rechts davon ein. Die dritte je nach Größe links, dazwischen oder rechts; und auch die folgenden Karten jeweils an der richtigen Stelle:

Hast du so schon einmal Karten sortiert?
Wenn ja, dann hast du intuitiv "Insertion Sort" angewendet (seltener: "Insertionsort", auf deutsch "Einfüge-Sortieren").
Insertion Sort Algorithmus
Kommen wir vom Kartenbeispiel zum Computeralgorithmus. Nehmen wir an, wir haben ein Array mit den Elementen [6, 2, 4, 9, 3, 7]. Dieses Array soll mit Insertion Sort aufsteigend sortiert werden.
Schritt 1
Zuerst teilen wir das Array gedanklich in einen linken, sortierten Teil und einen rechten, unsortierten Teil. Der sortierte Bereich enthält zu Beginn bereits das erste Element, da ein Array mit einem einzigen Element immer als sortiert angesehen werden kann.

Schritt 2
Dann betrachten wir das erste Element des unsortierten Bereichs und prüfen, an welcher Stelle im sortierten Bereich dieses eingefügt werden muss, in dem wir es mit seinem linken Nachbarn vergleichen.
Im Beispiel ist die 2 kleiner als die 6, gehört damit also links neben die 6. Um dort Platz zu machen, schieben wir die 6 um eine Position nach rechts und setzen die 2 dann auf das freigewordene Feld. Dann schieben wir die Grenze zwischen sortiertem und unsortiertem Bereich um eine Position nach rechts:

Schritt 3
Wir betrachten wieder das erste Element des unsortierten Bereichs, die 4. Diese ist kleiner als die 6, aber nicht kleiner als die 2 und gehört somit zwischen die 2 und die 6. Wir schieben also die 6 erneut um ein Feld nach rechts und setzen die 4 auf das freigewordene Feld:

Schritt 4
Das nächste zu sortierende Element ist die 9. Diese ist größer als ihr linker Nachbar 6, und damit größer als alle Elemente des sortierten Bereichs. Sie ist also bereits an der richtigen Stelle, so dass wir in diesem Schritt kein Element verschieben müssen:

Schritt 5
Das nächste Element ist die 3. Diese ist kleiner als die 9, die 6 und die 4, aber größer als die 2. Wir schieben daher die 9, 6 und 4 um je ein Feld nach rechts und setzen dann die 3 an die Stelle, an der die 4 zuvor war:

Schritt 6
Bleibt noch die 7 – sie ist kleiner als die 9, aber größer als die 6. Also schieben wir die 9 um ein Feld nach rechts und setzen die 7 auf die freigewordene Position:

Damit ist das Array fertig sortiert.
Insertion Sort Java Quellcode
Der folgende Java-Quellcode zeigt, wie einfach man Insertion Sort implementieren kann.
Die äußere Schleife iteriert – beginnend beim zweiten Element, da das erste ja bereits als sortiert gilt – über die einzusortierenden Elemente. Die Schleifenvariable i zeigt also immer auf das erste Element des rechten, unsortierten Teils.
In der inneren while-Schleife erfolgt die Suche nach der Einfügeposition und das Verschieben der Elemente kombiniert:
- das Suchen in der Schleifenbedingung: bis das Element links von der Suchposition
jkleiner ist als das einzusortierende Element, - und das Verschieben der sortierten Elemente im Schleifenrumpf.
public class InsertionSort {
public static void sort(int[] elements) {
for (int i = 1; i < elements.length; i++) {
int elementToSort = elements[i];
// Move element to the left until it's at the right position
int j = i;
while (j > 0 && elementToSort < elements[j - 1]) {
elements[j] = elements[j - 1];
j--;
}
elements[j] = elementToSort;
}
}
}Code-Sprache: Java (java)Der abgebildete Code unterscheidet sich in zwei Punkten vom Code im GitHub-Repository: Die Klasse InsertionSort im Repository implementiert zum einen das Interface SortAlgorithm, um innerhalb meines Testframeworks einfach austauschbar zu sein.
Zum anderen erlaubt sie die Angabe von Start- und Endindex, um auch Sub-Arrays sortieren zu können. Dies wird es uns später ermöglichen Quicksort zu optimieren, indem wir Teilarrays, die eine gewisse Größe unterschreiten, mit Insertion Sort sortieren lassen, anstatt diese weiter aufzuteilen.
Insertion Sort Zeitkomplexität
Wir bezeichnen die Anzahl der zu sortierenden Elemente mit n, im Beispiel oben wäre n = 6.
Die zwei ineinander verschachtelten Schleifen sind ein Indiz dafür, dass wir es mit quadratischem Aufwand zu tun haben, also mit einer Zeitkomplexität von O(n²)*. Das wäre dann der Fall, wenn sowohl die äußere als auch die innere Schleife bis zu einem Wert zählen, der linear mit der Anzahl der Elemente steigt.
Bei der äußeren Schleife ist das offensichtlich, da diese bis n zählt.
Und die innere Schleife? Diese analysieren wir in den nächsten drei Abschnitten.
* Die Begriffe "Zeitkomplexität" und "O-Notation" (ausgesprochen "Groß O-Notation") erkläre ich in diesem Artikel anhand von Beispielen und Diagrammen.
Zeitkomplexität im average case
Schauen wir uns noch einmal das Beispiel von oben an, in dem wir das Array [6, 2, 4, 9, 3, 7] sortiert haben.
Im ersten Schritt des Beispiels haben wir das erste Element als bereits sortiert definiert; im Quellcode wird dieses einfach übersprungen.
Im zweiten Schritt haben wir ein Element aus dem sortierten Array verschoben. Wäre das einzusortierende Element bereits an der richtigen Stelle gewesen, hätten wir nichts verschieben müssen. Das heißt, dass wir im Durchschnitt im zweiten Schritt 0,5 Verschiebe-Operationen haben.

Im dritten Schritt haben wir ebenfalls ein Element verschoben. Hier hätten es aber auch null oder zwei Verschiebungen sein können. Im Durchschnitt ist es in diesem Schritt eine Verschiebung.

In Schritt vier brauchten wir keine Elemente zu verschieben. Es hätten hier aber auch ein, zwei oder drei Verschiebungen nötig sein können, im Durchschnitt sind es hier 1,5.

In Schritt fünf haben wir im Durchschnitt zwei Verschiebe-Operationen:

Und im sechsten Schritt 2,5:

In Summe haben wir also durchschnittlich 0,5 + 1 + 1,5 + 2 + 2,5 = 7,5 Verschiebe-Operationen.
Das können wir auch wie folgt ausrechnen:
Sechs Elemente mal fünf Verschiebe-Schritte; geteilt durch zwei, da im Durchschnitt über alle Schritte die Hälfte der Karten bereits sortiert ist; und nochmal geteilt durch zwei, da das einzusortierende Element im Durchschnitt bis zur Mitte der bereits sortierten Elemente geschoben werden muss:
6 × 5 × ½ × ½ = 30 × ¼ = 7,5
Die folgende Grafik zeigt noch einmal alle Schritte:
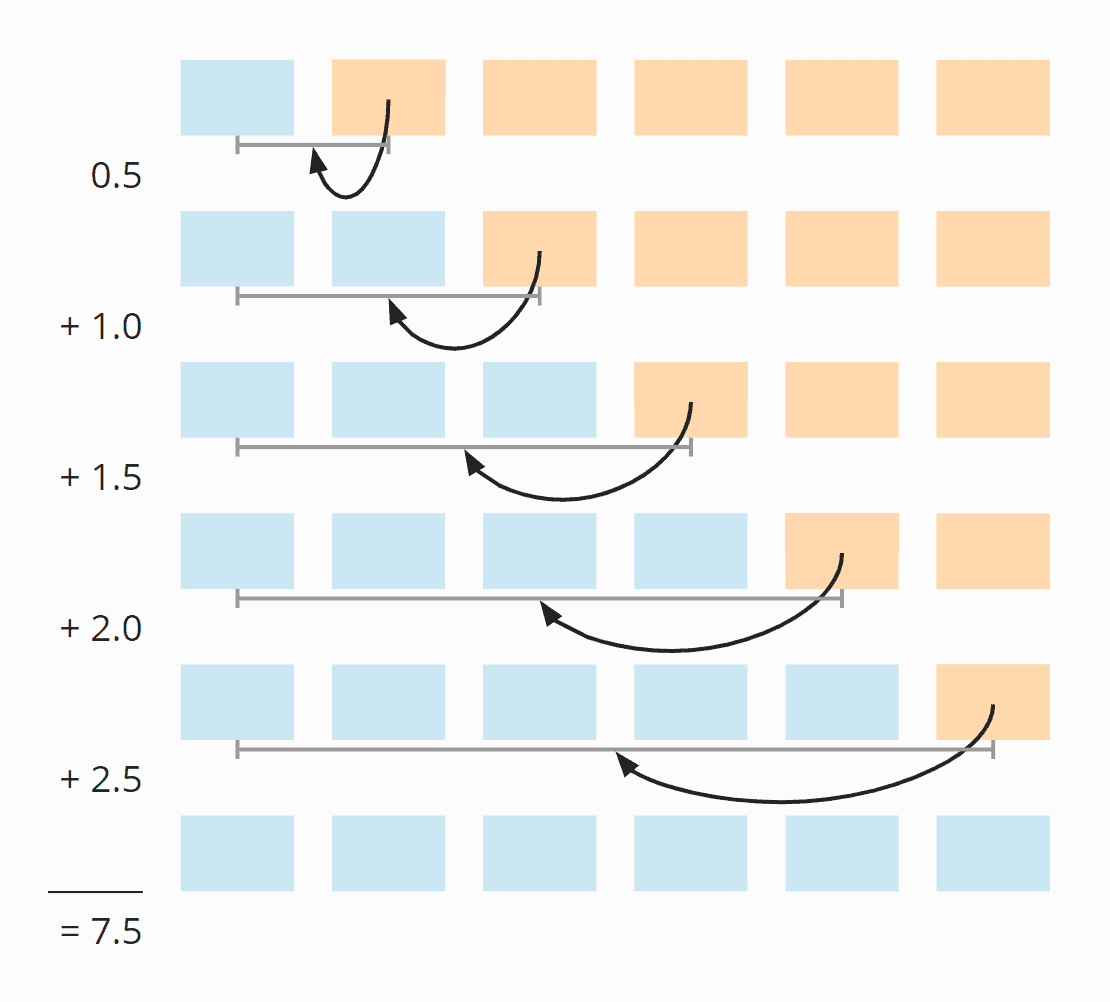
Ersetzen wir 6 durch n, erhalten wir:
n × (n - 1) × ¼
Ausmultipliziert ergibt das:
¼ n² - ¼ n
Die höchste Potenz von n in diesem Term ist n²; die Zeitkomplexität für das Verschieben beträgt daher O(n²). Dies wird auch als "quadratischer Aufwand" bezeichnet.
Wir haben bisher nur das Verschieben der sortierten Elemente betrachtet – doch was ist mit dem Vergleichen der Elemente und dem Setzen des zu sortierenden Elements auf das freigewordene Feld?
Vergleichsoperationen haben wir jeweils eine mehr als Vertauschoperationen (bzw. gleich viel, wenn bis ganz nach links geschoben wird). Die Zeitkomplexität für die Vergleichsoperationen ist damit ebenso O(n²).
Das einzusortierenden Element müssen wir genauso oft an die richtige Position setzen wie es Elemente gibt abzgl. derjenigen, die sich schon an der richtigen Stelle befinden. Also maximal n-1 mal. Da hier kein n² vorkommt, sondern nur ein n, sprechen wir von "linearerem Aufwand", notiert als O(n).
Bei der Betrachtung der Gesamtkomplexität zählt nur die höchste Komplexitätsstufe (s. a. "O-Notation und Zeitkomplexität – anschaulich erklärt"). Daher gilt:
Die Zeitkomplexität von Insertion Sort beträgt im average case: O(n²)
Wo es einen average case gibt, gibt es auch einen worst und einen best case.
Zeitkomplexität im worst case
Im worst case sind die Elemente zu Beginn komplett absteigend sortiert. In jedem Schritt müssen somit alle Elemente des sortierten Teil-Arrays nach rechts verschoben werden, damit das einzusortierende Element – welches in jedem Schritt kleiner ist als alle bereits sortierten Elemente – ganz an den Anfang gesetzt werden kann.
Im folgenden Diagramm wird dies dadurch demonstriert, dass die Pfeile immer nach ganz links zeigen.

Der Term aus dem average case ändert sich daher insofern, dass das zweite Teilen durch zwei wegfällt:
6 × 5 × ½
Bzw.:
n × (n - 1) × ½
Wenn wir dies ausmultiplizieren, erhalten wir:
½ n² - ½ n
Auch wenn wir nur halb so viele Operationen haben wie im durchschnittlichen Fall, ändert sich an der Zeitkomplexität nichts – der Term enthält immer noch ein n², und somit gilt:
Die Zeitkomplexität von Insertion Sort beträgt im worst case: O(n²)
Zeitkomplexität im best case
Der best case wird interessant!
Wenn die Elemente bereits in sortierter Reihenfolge vorliegen, gibt es in der inneren Schleife jeweils einen Vergleich und keine Vertauschoperation.
Bei n Elementen, also n-1 Schritten (da wir beim zweiten Element beginnen) kommen wir somit auf n-1 Vergleichsoperationen.
Die Zeitkomplexität von Insertion Sort beträgt somit im best case: O(n)
Insertion Sort mit binärer Suche?
Könnten wir den Algorihmus nicht beschleunigen, indem wir die Einfügeposition mit binärer Suche suchen? Diese ist doch deutlich schneller als die sequentielle Suche – sie hat eine Zeitkomplexität von O(log n).
Ja, das könnten wir. Allerdings hätten wir dadurch nichts gewonnen, da wir zum Verschieben trotzdem jedes Element ab der Einfügeposition um eine Position nach rechts verschieben müssten, was in einem Array eben nur schrittweise geht. Somit bliebe die innere Schleife trotz der binären Suche bei linearem Aufwand, der Gesamtalgorithmus also weiterhin bei quadratischem Aufwand, also O(n²).
Insertion Sort mit verketteter Liste?
Wenn die Elemente in einer verkettete Liste vorliegen, könnten wir dann nicht ein Element in konstanter Zeit, also O(1) einfügen?
Ja, das könnten wir. Allerdings erlaubt eine verkettete Liste keine binäre Suche. D. h. wir müssten in der inneren Schleife dennoch über alle sortierten Element iterieren, um die Einfügeposition zu finden. Womit wir wiederum bei linearem Aufwand für die innere Schleife wären – und damit bei quadratischem Aufwand für den Gesamtalgorithmus.
Laufzeit des Java Insertion Sort-Beispiels
Nach so viel Theorie wird es Zeit diese anhand der oben vorgestellten Java-Implementierung zu überprüfen.
Die Klasse UltimateTest aus dem GitHub-Repository führt Insertion Sort (und allen weiteren in dieser Artikelserie vorgestellten Sortieralgorithmen) wie folgt aus:
- für verschiedene Array-Größen, beginnend bei 1.024, dann jeweils verdoppelt bis 536.870.912 (der Versuch ein Array mit 1.073.741.824 Elementen zu erzeugen führt bei mir zu einem "Native memory allocation"-Fehler) – oder bis ein Test mehr als 20 Sekunden dauert;
- mit unsortierten, aufsteigend sortierten und absteigend sortierten Elementen;
- mit zwei Warm-Up-Runden, um dem HotSpot-Compiler zu ermöglichen den Code zu optimieren;
- danach so oft wiederholt, bis das Programm abgebrochen wird.
Nach jeder Wiederholung gibt das Testprogramm den Median der bisherigen Messergebnisse aus.
Hier das Ergebnis für Insertion Sort nach 50 Iterationen (dies ist der Übersicht halber nur ein Auszug; das vollständige Ergebnis findest du hier):
| n | unsortiert | absteigend | aufsteigend |
|---|---|---|---|
| ... | ... | ... | ... |
| 32.768 | 87,86 ms | 175,80 ms | 0,042 ms |
| 65.536 | 350,43 ms | 697,59 ms | 0,084 ms |
| 131.072 | 1.398,92 ms | 2.840,00 ms | 0,168 ms |
| 262.144 | 5.706,82 ms | 11.517,36 ms | 0,351 ms |
| 524.288 | 23.009,68 ms | 46.309,27 ms | 0,710 ms |
| 1.048.576 | – | – | 1,419 ms |
| ... | ... | ... | ... |
| 536.870.912 | – | – | 693,310 ms |
Man kann gut sehen,
- wie sich die Laufzeit bei Verdopplung der Eingabemenge bei unsortierten und absteigend sortierten Elementen in etwa vervierfacht,
- wie die Laufzeit im worst case doppelt so groß ist wie im average case,
- wie die Laufzeit bei vorab sortierten Elementen linear wächst und deutlich kleiner ist.
Die entspricht den erwarteten Zeitkomplexitäten O(n²) und O(n).
Hier die Messwerte noch einmal als Diagramm:

Bei aufsteigend vorsortierten Elementen ist Insertion Sort so schnell, dass die Kurve keinen sichtbaren Ausschlag nach oben zeigt. Hier daher die Kurve noch mal einzeln:

Weitere Eigenschaften von Insertion Sort
Die Platzkomplexität von Insertion Sort ist konstant, da wir außer den Schleifenvariablen i und j, sowie der Hilfsvariablen elementToSort keinen zusätzlichen Speicherplatz benötigen. D. h. egal ob wir 10 Elemente sortieren oder eine Million, wir benötigen immer nur diese drei zusätzlichen Variablen. Konstanten Aufwand notiert man als O(1).
Das Sortierverfahren ist stabil, da wir nur Elemente verschieben, die größer als das einzusortierende Element sind (nicht "größer oder gleich"), sich also die relative Position zweier gleicher Elemente zueinander nie ändert.
Insertion Sort ist nicht direkt parallelisierbar.* Allerdings gibt es eine parallelisierbare Variante von Insertion Sort: Shellsort (hier die Beschreibung auf Wikipedia).
* Man könnte binär suchen und dann das Verschieben der sortierte Elemente parallelisieren. Dies würde aber nur bei großen Arrays sinnvoll sein, die man genau entlang der Cache-Lines aufteilen müsste, um die durch die Parallelisierung gewonnene Performance durch Synchronisationseffekte nicht wieder zu verlieren bzw. ins Gegenteil umzudrehen. Diesen Aufwand spart man sich, da es für größere Arrays ohnehin effizientere Sortieralgorithmen gibt.
Insertion Sort vs. Selection Sort
Einen Vergleich der Laufzeiten von Insertion Sort und Selection Sort findest du im Artikel über Selection Sort.
Zusammenfassung
Insertion Sort ist ein sehr einfach zu implementierender, stabiler Sortieralgorithmus mit einer Zeitkomplexität von O(n²) im average und worst case, und O(n) im best case.
Für sehr kleine n ist Insertion Sort schneller als effizientere Algorithmen wie Quicksort oder Merge Sort, so dass diese Algorithmen kleinere Teilprobleme mit Insertion Sort lösen (die Dual-Pivot Quicksort-Implementierung in Arrays.sort() des JDK beispielsweise bei weniger als 44 Elementen).
Weitere Sortieralgorithmen findest du in dieser Übersicht aller Sortieralgorithmen und ihrer Eigenschaften im ersten Teil der Artikelserie.
