Generating Random Numbers in Java

Generating random numbers (or strings or other random objects) is one of the most common programming tasks.

This article describes:

• which possibilities there are in Java to generate random numbers,
• why these are so-called "pseudorandom numbers",
• what technology is behind their generation,
• how to predict random numbers in Java,
• and how the implementation of the various methods has changed throughout Java versions.

Experienced Java developers familiar with the various ways to create random values can skip directly to the "Pseudorandom Number Generation" or "Changes in Implementations Over Time" section.

You can find the code samples for this article in this GitHub repository.

How to Generate Random Numbers

This chapter shows the fundamental classes and methods for generating a random number in Java and what to consider when using them in terms of thread safety.

Java Math.random() Method

One of the oldest methods (it has existed since Java 1.0) to generate a random double number is to call Math.random():

double d = Math.random();Code language: Java (java)

The call returns a random number between 0 and 1. More precisely: a double floating-point number greater than or equal to 0.0 and less than 1.0.

Math.random() is thread-safe according to the documentation. However, synchronization is broken from Java 1.3 up to and including Java 7. If you work with one of these versions, you must not call Math.random() from different threads.

Internally, Math.random() calls the nextDouble() method of a static instance of the Random class held in the Math class, which is discussed in the next section.

For more details on Math.random()'s internal functionality and thread safety, see the chapter on implementing this method.

Java Random Class

Also present since Java 1.0 is the java.util.Random class. With it, you can generate a random int number as follows:

Random random = new Random();
int i = random.nextInt();Code language: Java (java)

The call returns a random integer number in the range of Integer.MIN_VALUE (= -2³¹ = -2.147.483.648) to Integer.MAX_VALUE (= 2³¹-1 = 2.147.483.647).

Other methods for generating random values are:

• nextInt(int bound) – generates a random number greater than or equal to 0 and less than the specified upper bound.
• nextLong() – generates a random long value.
• nextBoolean() – returns a random boolean value, i.e., true or false.
• nextFloat() – returns a random float number greater than or equal to 0.0 and less than 1.0.
• nextDouble() – returns a random double number greater than or equal to 0.0 and less than 1.0 (this method is called from Math.random(), as described in the previous section).
• nextBytes(byte[] bytes) – fills the specified byte array with random bytes.
• nextGaussian() – returns a Gaussian-distributed random number with a standard deviation of 1.0, i.e., according to the normal distribution, the probability of a number close to 0 is higher than the probability of a number far from 0.

You can use the setSeed(long seed) method or the second constructor Random(long seed) to set the so-called "seed" value of the random number generator. This is only necessary for special requirements. You can read more about this in the chapter on Pseudorandom Numbers.

Extensions to java.util.Random in Java 8

With the introduction of streams in Java 8, java.util.Random has been extended to include methods for generating random number streams. The Random.ints() method generates an IntStream: a stream of random int values.

The following example prints seven random numbers to the console:

Random random = new Random();
random.ints().limit(7).forEach(System.out::println);Code language: Java (java)

The limitation to seven elements set by limit(7) can also be requested in an overloaded variant of the ints() method:

Random random = new Random();
random.ints(7).forEach(System.out::println);Code language: Java (java)

Two further variants allow the specification of lower and upper bounds of the generated values. The following example generates seven random numbers greater than or equal to 0 and less than 1,000 – once limited by limits() and once by the first parameter of the ints() method.

Random random = new Random();
random.ints(0, 1000).limit(7).forEach(System.out::println);
random.ints(7, 0, 1000).forEach(System.out::println);Code language: Java (java)

Corresponding four variants exist for:

• longs() – generates a LongStream of random numbers
• doubles() – generates a DoubleStream of random numbers

Thread Safety of java.util.Random

java.util.Random is thread-safe, so you can safely call the methods of a single shared Random object from multiple threads.

Since the generated values are no true random numbers, but a random number is practically calculated from the previous one (this is very simplified; you can find more details in the chapter "Pseudorandom Numbers") – and since this calculation must be done atomically, the invocation of the method is subject to a certain synchronization overhead.

Many simultaneous invocations from multiple threads can thus harm performance. In the GitHub repo, you can find the program RandomMultipleThreadsDemo, demonstrating the difference.

The following graph shows how long it takes on my 6-core i7 to generate 100 million random numbers via a shared Random instance: about one second for one thread, over 50 seconds for six parallel threads:

I have measured the extreme case, in which the threads continuously generate random numbers, i.e., constantly cause contention (conflicts when accessing the shared state). If a thread generates a random number only occasionally, contention occurs less frequently and may not be measurable at all.

Provided you expect thread contention and your application does not require the use of a single random number generator (which should only be the case in exceptional cases), you can create a separate Random object per thread. Then the time for 100 million random numbers remains at about one second, no matter how many threads are running in parallel (MultipleRandomMultipleThreadsDemo in GitHub):

Better still is to use ThreadLocalRandom described in the following section.

Java ThreadLocalRandom Class

In Java 7, the java.util.concurrent.ThreadLocalRandom class was introduced. The static method ThreadLocalRandom.current() provides a random number generator for each thread independent of all other threads. This way, no thread contention can occur, and the synchronization overhead described in the previous section is eliminated.

ThreadLocalRandom.current() returns a ThreadLocalRandom object, which in turn inherits from Random and thus provides the same methods, e.g., nextInt():

Random random = ThreadLocalRandom.current();
int randomNumber = random.nextInt();Code language: Java (java)

The program ThreadLocalRandomMultipleThreadsDemo measures the performance of ThreadLocalRandom. The result: The generation of 100 million random numbers takes about 150 ms, no matter how many threads are running at the same time – an enormous performance gain compared to Random – not only with multiple threads but also with only one:

ThreadLocalRandom should, therefore, always be your first choice.

It is interesting to see how the implementation has changed fundamentally from Java 7 to Java 8. More about this in the section "Implementation of ThreadLocalRandom".

Generate a Random Number in a Range

A common requirement is to generate a random number from a specific range. You have already seen a few possibilities:

• Random.nextInt(int bound) – generates a random integer number between 0 and the specified upper bound.
• Random.ints(int randomNumberOrigin, int randomNumberBound) – generates an infinite stream of random numbers in the specified number range.
• Random.ints(long streamSize, int randomNumberOrigin, int randomNumberBound) – generates a stream of the specified number of random numbers in the specified number range.
• the analogous stream-generating methods Random.longs() and Random.doubles().

(The upper bound or randomNumberBound is always exclusive, i.e., the generated random numbers are always less than the specified maximum).

So we can

• either generate a single random number between 0 and an upper limit
• or a stream of random numbers constrained by lower and upper bounds.

However, if we want to generate a single random number from a range of numbers whose lower bound is not 0, we cannot use any existing JDK function but must take a roundabout route. Here are a few examples:

Random Number between 1 and 10

Since we can only define the upper bound of random numbers, we create a number between 0 and 9 and add a 1:

Random random = ThreadLocalRandom.current();
int number = 1 + random.nextInt(9);Code language: Java (java)

Attention: Upper bounds are always exclusive, i.e., the code returns a maximum of 9. To include 10, i.e., to get numbers less than or equal to 10, we have to modify the code as follows:

Random random = ThreadLocalRandom.current();
int number = 1 + random.nextInt(10);Code language: Java (java)

Random Number between 1 and 100

To generate a random number between 1 and 100, we generate a number between 0 and 99 and add 1:

Random random = ThreadLocalRandom.current();
int number = 1 + random.nextInt(99);Code language: Java (java)

Analogous to the previous example, we need to write nextInt(100) if we want to include 100.

Random Number between Two Values

If we need a random number between two given values more often, we should extract the generation to a helper method:

public class RandomUtils
  public static int nextInt(Random random, int origin, int bound) {
    if (origin >= bound) {
      throw new IllegalArgumentException();
    }
    return origin + random.nextInt(bound - origin);
  }
}Code language: Java (java)

We can then call this, for example, as follows to generate a random number between 1 and 6 inclusive:

Random random = ThreadLocalRandom.current();
int randomNumberFrom1To6 = RandomUtils.nextInt(random, 1, 7);Code language: Java (java)

This way, you can simulate the roll of a die, for example.

How to Generate a Random String in Java

So far, we have learned about methods of the Random class that allow us to create random integers (nextInt), random doubles (nextDouble), random arrays (nextBytes), and random booleans (nextBoolean).

However, sometimes we need a random string – that is, a string filled with a random or specific number of random characters.

We can do this by gradually filling a StringBuilder with random lowercase letters (you can find this and the following methods in the RandomUtils class in GitHub):

public static String randomLowerCaseString(int length) {
  StringBuilder sb = new StringBuilder();
  Random r = ThreadLocalRandom.current();
  for (int i = 0; i < length; i++) {
    char c = (char) ('a' + r.nextInt(26));
    sb.append(c);
  }
  return sb.toString();
}Code language: Java (java)

It gets a bit more complicated if we want to extend the character range, e.g., to upper case letters, numbers, and the space character. Then we have to define an alphabet and pick a random character from it:

private static final String ALPHANUMERIC_WITH_SPACE_ALPHABET =
    " 0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz";

public static String randomAlphanumericalWithSpaceString(int length) {
  return randomString(length, ALPHANUMERIC_WITH_SPACE_ALPHABET);
}

public static String randomString(int length, String alphabet) {
  StringBuilder sb = new StringBuilder();
  Random r = ThreadLocalRandom.current();
  for (int i = 0; i < length; i++) {
    int pos = r.nextInt(alphabet.length());
    char c = alphabet.charAt(pos);
    sb.append(c);
  }
  return sb.toString();
}Code language: Java (java)

Since Java 8, we can also implement the randomString() method using a stream:

public static String randomStringWithStream(int length, String alphabet) {
  return ThreadLocalRandom.current()
      .ints(length, 0, alphabet.length())
      .map(alphabet::charAt)
      .collect(StringBuilder::new, StringBuilder::appendCodePoint, StringBuilder::append)
      .toString();
}Code language: Java (java)

Alternatively, you can use one of the numerous methods of the RandomStringUtils class from the open-source Apache Commons Lang project.

Pseudorandom Number Generation in Java

This article has mentioned the topic of "pseudorandom numbers" a few times already, and now it is time to take a closer look at the subject.

As briefly mentioned before, Random does not generate truly random numbers. It can't because computers are based on algorithms, and algorithms are concrete rules that lead from a specific input to a particular output.

What is generated instead are so-called "pseudorandom numbers". These are based on a sequence of numbers that starts at a specific value (the so-called "seed") and where the next number is calculated from the previous one.

The algorithm is constructed in such a way that the generated numbers a) give the impression of being random and b) are evenly distributed in the number space (you can read the mathematical theory behind this in the Wikipedia article "Linear congruential generator").

Seed Value

The starting value "seed" is generated from the system time when the Random() constructor is called. This makes it highly probable that the random number sequence will start at a different position each time a Random object is created.

But we can also set the seed value ourselves:

• in the constructor Random(long seed)
• or with the method setSeed(long seed)

When we do that, we always get the same sequence of random numbers. We can check this quite easily: The following code (class SetSeedExample in GitHub) prints the sequence of numbers 30, 63, 48, 84, 70 twice every time it is started – on any operating system and with any Java version.

Random random = new Random(42);
for (int i = 0; i < 5; i++) {
  System.out.println(random.nextInt(100));
}

random.setSeed(42);
for (int i = 0; i < 5; i++) {
  System.out.println(random.nextInt(100));
}Code language: Java (java)

Why doesn't the number sequence start at 42?

You will find the answer in the next section.

Deriving Random Numbers from the Random Number Generator’s State

The "seed" value does not determine the first random number but the starting state of the random number generator. In the Random class, the state is stored in a 48-bit number calculated from the "seed".

Inappropriately, the state is stored in a variable that also has the name seed; the name state would have been more appropriate. The respective subsequent state is calculated using the following formula:

seed = (seed * 25.214.903.917 + 11) & 2⁴⁸-1

From this 48-bit value, as many bits are then taken left-justified as are required for the requested random value, e.g., 32 bits for an int:

… or 1 bit for a boolean:

And for numbers that require more than 48 bits, like long or double?

• For a long, 32 bits are picked, then the next state is calculated, then another 32 bits are picked.
• For a double, 26 bits are taken first and then another 27 bits, resulting in 53 bits (which corresponds to the precision of a double value).

Never more than 32 bits are taken from the 48 bits. Why is the status then 48 bits long and not 32?

The reason is the following:

If the status were only 32 bits long, any given random integer would always be followed by the same successor. This, in turn, means that a single random number would be enough to predict all future random numbers.

Because the remaining 16 bits are hidden for a 48-bit status, there are 2¹⁶ possible statuses for a 32-bit value, i.e., 65,536 different statuses in which the random number generator could currently be. So, the same random integer number can have 65,536 different successors, and this makes a prediction from a single number impossible.

However, if we know two consecutive random numbers, the situation is quite different. More about this in the section "Predictability of random numbers".

Generating Pseudorandom Numbers in java.util.Random

What does this look like in java.util.Random's source code?

Let's start with the nextInt() method:

public int nextInt() {
    return next(32);
}Code language: Java (java)

The invoked next() method looks like this.

(I have printed the original implementation up to Java 1.3 because it is the easiest to understand. You can find the latest – optimized, but functionally identical – implementation chapter "Changes in Implementations over Time" below.)

private static final long multiplier = 0x5DEECE66DL;
private static final long addend = 0xBL;
private static final long mask = (1L << 48) - 1;

// ...

synchronized protected int next(int bits) {
    long nextseed = (seed * multiplier + addend) & mask;
    seed = nextseed;
    return (int)(nextseed >>> (48 - bits));
}
Code language: Java (java)

Line 8 implements the formula presented in the previous section for calculating the subsequent state.

In line 10, the requested bits are extracted by "right shift" and casting to an int. The following graphic illustrates this for 32 bits:

… and once for 1 bit:

The nextBoolean() method then only has to check whether the 1-bit number thus obtained is 1 or 0:

public boolean nextBoolean() {
    return next(1) != 0;
}Code language: Java (java)

The nextLong() method, as mentioned above, first gets 32 bits, shifts them 32 bits to the left, and adds a second 32-bit number:

public long nextLong() {
    return ((long)(next(32)) << 32) + next(32);
}Code language: Java (java)

The nextDouble() method is a bit more complicated (again, first the – somewhat easier to read, since not yet highly optimized – original implementation up to Java 7):

public double nextDouble() {
    long l = ((long)(next(26)) << 27) + next(27);
    return l / (double)(1L << 53);
}Code language: Java (java)

The method performs the following two steps:

1. Concatenation of a 26-bit random number with a 27-bit random number to form a 53-bit number (i.e., a number between 0 and 2⁵³-1).
2. Division by 2⁵³ (one more than the highest number that could be generated in step 1).

This then results in a number >= 0.0 and < 1.0.

Why are only 53 bits used for a double and not 64? The reason is that double-precision floating-point numbers use 53 bits for sign and fraction and 11 bits for the exponent. You can find a more detailed explanation in the Wikipedia article "Double-precision floating-point format".

Similarly, the nextFloat() method uses 24 bits and not 32 (see Wikipedia article "Single-precision floating-point format"):

public float nextFloat() {
    return next(24) / ((float)(1 << 24));
}Code language: Java (java)

Predictability of Random Numbers

In the penultimate section, I claimed that we could predict from two consecutive pseudorandom numbers which subsequent numbers will follow. We can verify this assertion with a simple test.

The program RandomIntegerPairRepetitionFinder generates all 2¹⁶ possible seed values for each of the 2³² integer numbers – and from these their 2¹⁶ potential successors. If the program finds the same pair of consecutive pseudorandom numbers more than once, it prints this to the console.

After 24 hours, no repetition was found on my laptop. However, the program would have to run for almost 1,200 hours, or 50 days, to check all combinations. I don't have that much time, so I can't prove my claim.

Nevertheless, we can write a program that predicts all further random numbers from two given ones. Such a program can detect if there is only one possible sequence for the input – and ask for a third number if two are not enough.

How to Predict the Next Random Number in Java

Given two random numbers generated by Random.nextInt(), predicting the subsequent random numbers is relatively easy.

To do this, we determine the 2¹⁶ possible seed values for the first given number, generate the respective successor for each and check whether it matches the second given number. If this is the case, we can calculate all subsequent random numbers based on the seed value determined in this way.

You can find the complete code for this in the RandomIntegerPredictor class.

The following code shows the method that determines the seed value. I have simplified it for printing in this article to use only two input numbers. The code in the linked class can also handle a longer input sequence.

private static final int NUMBER_OF_POSSIBLE_SEEDS = 1 << 16;

private static final long multiplier = 0x5DEECE66DL;
private static final long addend = 0xBL;
private static final long mask = (1L << 48) - 1;

// ...

private long getSeedMatchingForSequence() {
  long firstNumberSeedBase = Integer.toUnsignedLong(givenNumbers[0]) << 16;

  for (int noise = 0; noise < NUMBER_OF_POSSIBLE_SEEDS; noise++) {
    long seed = firstNumberSeedBase | noise;
    long nextSeed = getNextSeed(seed);
    int nextInt = (int) (nextSeed >>> 16);
    if (nextInt == givenNumbers[1]) {
      return seed;
    }
  }

  throw new IllegalArgumentException(
      "Found no matching seed; please verify your input sequence.");
}

private long getNextSeed(long seed) {
  return (seed * multiplier + addend) & mask;
}Code language: Java (java)

From the seed value thus obtained, we can derive the further sequence of numbers:

public int[] predict(int numberOfPredictions) {
  long seed = getSeedMatchingForSequence();

  // Skip the given numbers
  for (int i = 0; i < givenNumbers.length; i++) {
    seed = getNextSeed(seed);
  }

  // Get the predictions
  int[] predictions = new int[numberOfPredictions];
  for (int i = 0; i < numberOfPredictions; i++) {
    predictions[i] = (int) (seed >>> 16);
    seed = getNextSeed(seed);
  }

  return predictions;
}Code language: Java (java)

The GitHub contains a demo, RandomIntegerPredictorDemo, which prints two random numbers, predicts the following ten random numbers, and finally prints ten more random numbers. The prediction is correct:

Two random numbers:
-1,179,305,299
435,136,901

Predicting 10 random numbers:
-2,139,482,012
1,388,148,251
1,134,856,645
-1,205,820,716
182,240,689
...

Next *actual* random numbers:
-2,139,482,012
1,388,148,251
1,134,856,645
-1,205,820,716
182,240,689
...Code language: plaintext (plaintext)

The repo also contains the RandomIntegerPredictorRunner command line runner, which you can call (after compiling the code) as follows:

$ java eu.happycoders.random.predictor.RandomIntegerPredictorRunner 5 999571443 25208007
Given numbers: [999571443, 25208007]
Predicting 5 random numbers...
-1,315,941,039
136,476,741
1,077,533,899
-211,240,302
143,354,061
Code language: plaintext (plaintext)

The first parameter, 5, specifies how many subsequent numbers to display; the following parameters are the known sequence of random numbers. The output is the prediction of the subsequent random numbers.

Java SecureRandom Class

In the last section of the previous chapter, you learned how to predict all subsequent random numbers from only two consecutive ones.

For certain requirements (e.g., cryptography), this predictability is not acceptable. In such cases, we need a "secure" random number generator.

The class java.security.SecureRandom has been available since Java 1.1. It generates "cryptographically strong" random numbers as defined in RFC 1750 "Randomness Recommendations for Security".

"Cryptographically strong" can be implemented in one of the following two ways (or a combination of both):

• A deterministic sequence like Random, but with much larger "noise" (the bits from the seed not included in the generated random number), so that reverse-engineering the seed from a given sequence becomes virtually impossible with today's hardware.
• Truly random numbers generated by a special hardware that measures, for example, radioactive decay processes.

Different types of secure random number generators can be made available through the Java Service Provider Interface (SPI) and selected at runtime via SecureRandom.getInstance(String algorithm) and some overloaded variants of this method.

The constructor of SecureRandom provides a default implementation. SecureRandom inherits from Random and thus provides the same methods. The following example shows how you can generate a secure random floating-point number:

SecureRandom secureRandom = new SecureRandom();
double strongRandomNumber = secureRandom.nextDouble();Code language: Java (java)

You can find more details in the SecureRandom JavaDoc.

Changes in Implementations over Time

In this section, you will learn how the random number generation methods presented in this article are implemented and how (and why) the implementations have been revised over the course of Java versions.

Implementation of Math.random()

The static method Math.random() internally calls the nextDouble() method on a static instance of the Random class. The code for creating the static Random object has been changed several times.

In Java 1.0, the Math.random() method was simply provided with the synchronized keyword. That was correct but led to a high synchronization overhead:

public static synchronized double random() {
    if (randomNumberGenerator == null)
        randomNumberGenerator = new Random();
    return randomNumberGenerator.nextDouble();
}Code language: Java (java)

Java 1.3 switched to the "Double-checked locking" pattern:

// !!! DON'T DO THIS - NOT THREAD-SAFE !!!

public static double random() {
    if (randomNumberGenerator == null) initRNG();
    return randomNumberGenerator.nextDouble();
}

private static synchronized void initRNG() {
    if (randomNumberGenerator == null) 
        randomNumberGenerator = new Random();
}Code language: Java (java)

This supposedly more performant implementation is not thread-safe! Due to the unsynchronized read access to randomNumberGenerator in the random() method, a thread could see an incompletely initialized object at this point. You can find a detailed explanation in the Wikipedia article linked above.

Only in Java 8 this error was recognized, and the implementation was changed to the "Initialization on Demand Holder" pattern:

private static final class RandomNumberGeneratorHolder {
    static final Random randomNumberGenerator = new Random();
}

public static double random() {
    return RandomNumberGeneratorHolder.randomNumberGenerator.nextDouble();
}Code language: Java (java)

In this pattern, randomNumberGenerator is not created until it is needed; and the JVM guarantees proper synchronization when initializing the RandomNumberGeneratorHolder class.

Nothing else has changed in this implementation until Java 18.

Implementation of java.util.Random

In the chapter "Pseudorandom Numbers in Java", I explained the basic implementation of the Random class using its Java 1.0 source code. The public methods internally call the next(int bits) method.

Its synchronization was originally done via the synchronized keyword, which is easy to use, but – especially up to and including Java 5 – caused a high performance impact.

Here, once again, the code from Java 1.0:

private long seed;

synchronized protected int next(int bits) {
    long nextseed = (seed * multiplier + addend) & mask;
    seed = nextseed;
    return (int)(nextseed >>> (48 - bits));
}Code language: Java (java)

In Java 1.4, the seed value was stored in a (then internal) sun.misc.AtomicLong and changed with attemptUpdate(). This method uses compare-and-set, i.e., optimistic locking:

import sun.misc.AtomicLong;

private AtomicLong seed;

protected int next(int bits) {
    long oldseed, nextseed;
    do {
      oldseed = seed.get();
      nextseed = (oldseed * multiplier + addend) & mask;
    } while (!seed.attemptUpdate(oldseed, nextseed));
    return (int)(nextseed >>> (48 - bits));
}Code language: Java (java)

Java 5 moved to the new, official java.util.concurrent.atomic.AtomicLong and its compareAndSet() method:

import java.util.concurrent.atomic.AtomicLong;

private AtomicLong seed;

protected int next(int bits) {
    long oldseed, nextseed;
    AtomicLong seed = this.seed;
    do {
        oldseed = seed.get();
        nextseed = (oldseed * multiplier + addend) & mask;
    } while (!seed.compareAndSet(oldseed, nextseed));
    return (int)(nextseed >>> (48 - bits));
}Code language: Java (java)

In Java 6, the AtomicLong variable was made final. Until Java 18, the implementation of the next() method was not changed again.

Another change was made to the nextDouble() method. As a reminder – this is what it initially looked like:

public double nextDouble() {
    long l = ((long)(next(26)) << 27) + next(27);
    return l / (double)(1L << 53);
}Code language: Java (java)

Since division is much more expensive than multiplication, in Java 8, the value 1/2⁵³ was extracted into a constant and is since used as a multiplication factor:

private static final double DOUBLE_UNIT = 0x1.0p-53; // 1.0 / (1L << 53)

public double nextDouble() {
    return (((long)(next(26)) << 27) + next(27)) * DOUBLE_UNIT;
}Code language: Java (java)

The functionality of the Random class has thus remained unchanged since Java 1.0. Up to Java 8, however, its performance has improved continuously.

Implementation of java.util.concurrent.ThreadLocalRandom

In Java 7, the ThreadLocalRandom.current() method returns a separate instance of ThreadLocalRandom per thread:

private static final ThreadLocal<ThreadLocalRandom> localRandom =
    new ThreadLocal<ThreadLocalRandom>() {
        protected ThreadLocalRandom initialValue() {
            return new ThreadLocalRandom();
        }
};

public static ThreadLocalRandom current() {
    return localRandom.get();
}Code language: Java (java)

ThreadLocalRandom inherits from Random, which stores the state in an AtomicLong. Since its thread safety (and the resulting overhead) are not needed in ThreadLocalRandom, ThreadLocalRandom keeps the state in its own field rnd instead, which it accesses without synchronization:

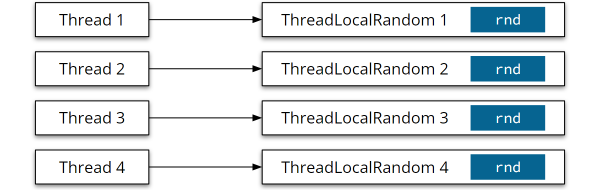
In Java 8, ThreadLocalRandom has been completely rewritten. Instead of providing separate instances per thread, ThreadLocalRandom.current() returns the same static instance of ThreadLocalRandom for all threads.

To prevent all threads from accessing the same state (which would then have to be synchronized again), the state is stored in the threadLocalRandomSeed variable of the current thread's Thread object:

This field is accessed from ThreadLocalRandom via jdk.internal.misc.Unsafe:

private static final Unsafe U = Unsafe.getUnsafe();
private static final long SEED
    = U.objectFieldOffset(Thread.class, "threadLocalRandomSeed");

// ...

final long nextSeed() {
    Thread t; long r; // read and update per-thread seed
    U.putLong(t = Thread.currentThread(), SEED,
              r = U.getLong(t, SEED) + (t.getId() << 1) + GOLDEN_GAMMA);
    return r;
}
Code language: Java (java)

You can easily show that different threads use different ThreadLocalRandom instances in Java 7 and the same ThreadLocalRandom instance in Java 8 with the following code:

for (int i = 0; i < 3; i++) {
  new Thread() {
    @Override
    public void run() {
      System.out.println(
          "ThreadLocalRandom instance: " + ThreadLocalRandom.current());
    }
  }.start();
}Code language: Java (java)

If you run the code under Java 7, you will see three different instances; under Java 8, you will see the same instance three times.

Implementation of java.secure.SecureRandom

SecureRandom is not itself an implementation of a secure random number generator. Concrete implementations are provided via the Service Provider Interface (SPI). Going into these is beyond the scope of this article.

Two enhancements to SecureRandom itself are worth mentioning:

• In Java 1.5, the getAlgorithm() method was added, returning the name of the implemented algorithm.
• In Java 8, the static getInstanceStrong() method was added, returning the implementation of a particularly strong algorithm, such as those recommended for RSA key pairs.

"Enhanced Pseudo-Random Number Generators" in Java 17

In Java 17, the random number generators in the JDK have been extended with an interface hierarchy to allow for future extensions. You can find details about this in the article about Java 17.

Summary

This article started by showing the various ways to generate random numbers in Java.

After that, you learned why random numbers are actually pseudorandom numbers, how to calculate a sequence of random numbers, and how to predict all future random numbers from two given random numbers.

The article concluded with a journey through Java versions and in it showed how (and why) the implementations of the previously shown methods have changed over time.

If you liked the article, feel free to leave a comment and share it using one of the share buttons at the end. If you want to be informed about new articles on HappyCoders.eu, click here to sign up for the HappyCoders newsletter.